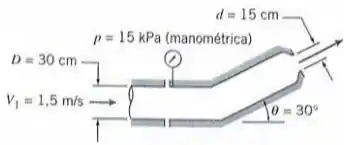
Água escoa em regime permanente através do bocal mostrado, descarregando para atmosfera. Calcule a componente horizontal da força na junta flangeada.
Passo 1
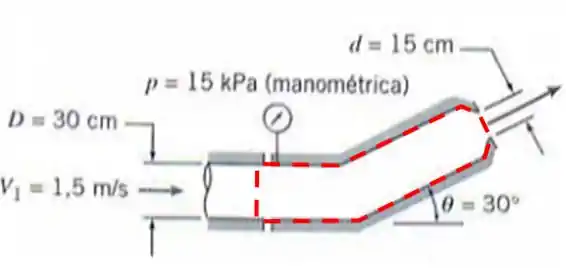
Novamente, o primeiro passo é escolher o volume de controle. Que nesse caso será o próprio bocal. Assim:
Essa questão temos que nos atentar ao fato da pressão dentro do bocal ser diferente da de quando ele sai. Assim temos uma força de pressão que não podemos esquecer.
Além disso não sabemos a velocidade de saída e para descobrir isso vamos usar a conservação de massa, isso mesmo o que aprendemos na teoria passada vai servir de auxilio nessa e nas demais teorias.
E depois disso iremos montar a equação de momento linear.
Passo 2
Vamos começar calculando a força de pressão. Vimos na teoria que se a pressão for constante:
Assim, como temos pressão e área constante, a nossa força de pressão será:
Agora, vamos calcular a velocidade de saída do fluido. Para isso vamos lembrar que o principio de conservação de massa, nos fornecia que o fluxo de massa que entra em um sistema incompressível e permanente deve ser igual ao fluxo de massa que sai.
Assim, chegávamos na equação:
Como a velocidade e a seção reta de entrada e de saída são constantes, podemos abrir a vazão em .
Cortando a densidade e substituindo os valores que conhecemos temos:
Porém essa velocidade é na direção de , iremos precisar da velocidade apenas na direção , assim iremos decompor essa velocidade:
Passo 3
Beleza, agora vamos aplicar a equação de momento linear:
As forças atuando serão a força que atua no boca e é ela que queremos descobrir e a força de pressão. Assim temos:
As vazões mássica a gente já viu que são iguais assim,
Voltando para a equação de momento, temos: