Qual das opções abaixo se refere a uma equação do terceiro grau?
Passo 1
Bom, vamos lá!! Vamos analisar cada uma das opções e verificar qual delas teremos uma equação do terceiro grau?!

Lembrando que em uma equação do terceiro grau precisamos que a maior variável seja a variável elevada ao expoente 3, beleza?!
Passo 2
a) De cara já podemos descartar a letra (a), pois o termo de maior grau é o . Logo, é uma equação do primeiro grau!

b) Aqui também temos a equação geral de uma equação geral do segundo grau, então não é a opção que estamos procurando!
Passo 3
c) Nessa opção temos . Como podemos verificar qual o grau dessa equação?
Podemos fazer a multiplicação distributiva aqui:
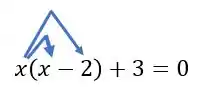
Assim, ficamos com
Ou seja, temos uma equação do segundo grau! Logo, não é a opção que estamos procurando!
Passo 4
d) Bom... só nos resta essa opção. Vamos verificar se de fato essa é uma equação do terceiro grau? Como temos podemos fazer a distributiva.
- Primeiro faremos a multiplicação da parte que está em vermelho
- Agora faremos a multiplicação da parte azul e em seguida da amarela
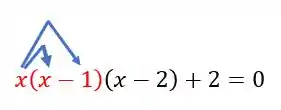
Fazendo a multiplicação dos termos em vermelho, temos
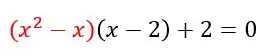
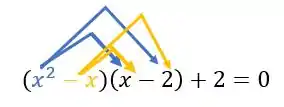
Ficando com
![]()
OPA!! Já vimos que surgiu um termo ali que é o de maior grau da equação! Então, encontramos a nossa equação do terceiro grau!
Se quiser podemos dar uma arrumada e somar os termos que tem na equação que encontamos
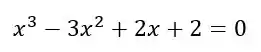
Ou seja, a nossa resposta é a letra (d)!!