Um capacitor está conectado a um resistor e a uma fonte de voltagem alternada como mostrado na figura. A fonte fornece uma fem dada por . As placas do capacitor são discos de raio . O ponto está entre duas placas, equidistante destas e a uma distância do centro do eixo de simetria. De acordo com a teoria eletromagnética, no ponto
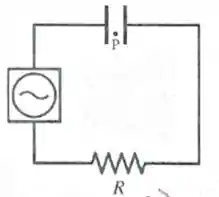
- Não há campo magnético porque não existe carga se movendo entre as placas.
- Existe um campo magnético constante.
- Existe uma corrente de elétrons fluindo.
- Existe um campo elétrico constante no tempo.
- Existe um campo magnético variável no tempo.
Passo 1
Aqui precisamos ter em mente que a teoria eletromagnética diz que um campo magnético variável no tempo gera um campo elétrico:
e também que que um campo elétrico variável no tempo produz um campo magnético :
Passo 2
O potencial dependente do tempo envia cargas que vão se acumulando sobre as placas do capacitor e, por essa razão, a carga do capacitor varia no tempo também. Consequentemente, o campo elétrico produzido por essas cargas e que está dentro das placas também depende do tempo:
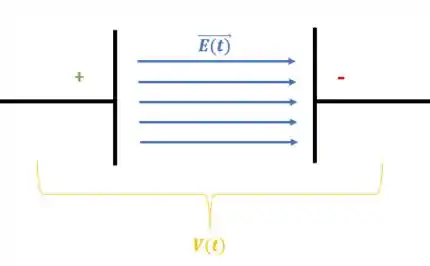
Se o campo elétrico é variável e alterna no tempo na região entre as placas, então o fluxo de campo elétrico varia no tempo:
Então, também haverá um campo magnético na região onde está o ponto que irá variar no tempo:
Através da equação:
Resposta
e) Existe um campo magnético variável no tempo.