Um capacitor de placas circulares paralelas está sendo carregado. Calcule o raio das duas placas, sabendo que o raio das duas placas são iguais, a taxa de variação temporal do campo elétrico é igual a e que a intensidade do campo magnético gerado pela variação do campo elétrico é . Dados: a constante de permissividade elétrica no vácuo é e o coeficiente de permeabilidade magnética no vácuo é
Passo 1
Vamos começar relembrando a Lei Ampère- Maxwell:
Se pensarmos em um caminho fechado em torno de uma das placas do capacitor de placa circular, podemos fazer uma curva de mesmo raio que a placa:
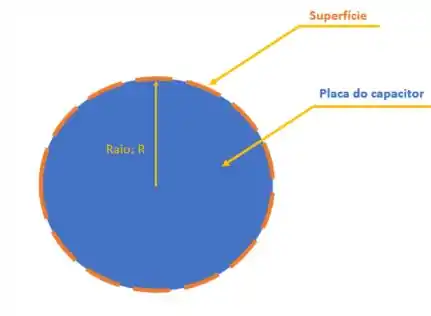
Logo o caminho da superfície dependerá do raio da placa do capacitor:
Passo 2
Integrando o campo magnético nessa superfície será o produto entre o campo magnético e a integral do raio:
Vamos pensar em módulos, pois foi isso que foi dado no enunciado, beleza? Então nossa equação se tornou:
Passo 3
Pense comigo, entre duas placas de um capacitor, não existe corrente elétrica, pois não é ligação física, porém ocorre passagem de fluxo elétrico, logo:
Então a equação fica da forma:
Passo 4
O fluxo de campo elétrico nada mais é do que o campo elétrico dividido pela área da placa:
Em um capacitor de placa circular, a área será a área do círculo, que é igual a:
Substituindo na equação do fluxo elétrico:
Nossa equação fica da seguinte forma então:
Como o que varia no tempo é apenas o campo elétrico e não o raio , podemos retirar da derivada:
Passo 5
Vamos organizar essa igualdade que parece um pouco bagunçada:
Primeiro, vamos ver que esse produto pela fração, teremos:
Como temos dos dois lados da igualdade, podemos cortar esse valor em ambos os lados:
Sabemos que:
Então:
Como temos dos dois lados da equação, podemos cortar de cada lado da igualdade:
Passo 6
Vamos substituir os valores que foram dados no enunciado:
Nossa equação:
Com os valores se torna:
Como apenas não sabemos o raio , vamos passar tudo que multiplica para o outro lado:
Vamos realizar as multiplicações no numerador e no denominador:
Substituindo na equação:
Como temos multiplicando no numerador e no denominador, podemos cortar:
O produto entre potências de mesma base, mantemos a base a somamos os expoentes:
Sabemos que qualquer número elevado a zero é igual a :
Logo a igualdade se torna:
Dividindo por temos o raio :
Não podemos esquecer que o raio é dado em metros!