Uma barra fina rígida de massa distribuída de maneira uniforme em seu comprimento tem uma de suas extremidades presas a um suporte no teto. A barra é mantida em repouso sob a ação de uma força constante , que atua na sua extremidade livre, perpendicular à direção da barra, conforme mostra a figura. Observa-se que a barra forma um ângulo com a direção vertical.
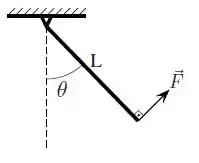
Qual o módulo da força exercida sobre a barra?
(a)
(b)
(c)
(d)
(e)
(f) Não é possível a barra permanecer em repouso nessa configuração.
(g)
(h)
Passo 1
Essa é uma questão de equilíbrio estático.
Para que a barra esteja em repouso, tanto a força quanto o torque resultantes sobre ela são nulos:
Mas repara que existe outra força que não conhecemos além de .
É a força normal no suporte da barra...
Como não conhecemos ela, uma boa saída é calcular o torque resultante com relação a exatamente esse ponto do suporte da barra.
OBS: O torque resultante com relação a qualquer ponto da barra é nulo, por isso podemos escolher o mais conveniente.
Isso porque dessa maneira, o torque dessa força normal desconhecida será nulo e sairá da equação.
Passo 2
Então, vamos calcular o torque com relação ao ponto de suporte da barra.
A força peso está aplicada no centro de massa da barra, já que ela é uniforme:
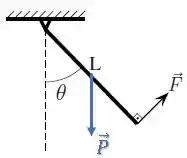
Vamos decompor essa força nas componentes paralela e perpendicular à barra:
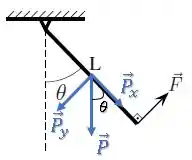
Passo 3
A componente não gera torque pois está na direção passando pelo eixo de rotação da barra.
Tanto a componente quanto a força estão perpendiculares à barra.
gera um torque no sentido horário enquanto gera um torque no sentido anti-horário, logo eles se cancelam:
Passo 4
As distância do eixo de rotação até o ponto de aplicação de é igual a metada do comprimento da barra.
Já a distância do mesmo até o ponto de aplicação da força é igual ao comprimento da barra, então:
Ficamos com a letra (g).
Resposta
Letra (g)