Para quebrar a casca de uma noz com um quebra-nozes, forças de pelo menos de módulo devem agir sobre a casca em ambos os lados. Para o quebra-nozes da figura abaixo, com distâncias e . Quais são as componentes das forças em cada cabo (aplicadas perpendicularmente aos cabos) que correspondem a esses ?
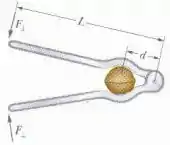
Passo 1
Vamos aplicar o equilíbrio do torque resultante.
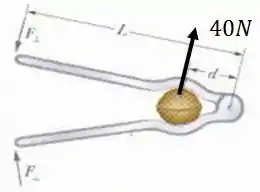
Uma força de age sobre a casa a uma distância . Precisamos descobrir o valor da força a uma distância .
Vamos aplicar a fórmula do torque resultante, escolhendo o ponto de encontro entre os dois cabos como eixo de rotação.
A força é perpendicular a distância e gera torque no sentido anti-horário.
A força de é perpendicular a distância e gera torque no sentido horário.
Definindo por convenção o sentido anti-horário como positivo, montamos a equação.
=0