Na figura abaixo, um bloco de é mantido em repouso através de um sistema de polias. O braço da pessoa está na vertical; o antebraço faz um ângulo com a horizontal. O antebraço e a mão têm uma massa conjunta de com um centro de massa a uma distância à frente do ponto de contato dos ossos do antebraço com o osso do braço (úmero). Um músculo (o tríceps) puxa o antebraço verticalmente para cima com uma força cujo ponto de aplicação está a uma distância atrás desse ponto de contato. A distância é . Quais são:
- O módulo da força exercida pelo tríceps sobre o antebraço
- O sentido (para cima ou para baixo) da força exercida pelo tríceps sobre o antebraço
- O módulo da força exercida pelo úmero sobre o antebraço
- O sentido (para cima ou para baixo) da força exercida pelo úmero sobre o antebraço
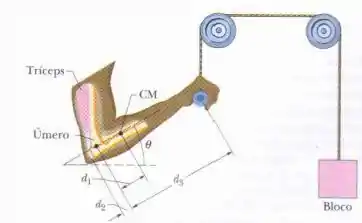
Passo 1
Como o bloco é mantido em repouso, podemos usar a equação de equilíbrio estável do torque.
Utilizando o ponto de contato dos ossos do antebraço com o osso do braço (úmero) como eixo de rotação, podemos aplicar:
Para aplicar essa fórmula, vamos achar as distâncias perpendiculares com a linha de ação das forças e calcular os momentos.
:
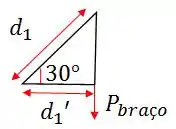
é a distância perpendicular do eixo de rotação até o centro de massa em que o peso do antebraço e da mão atuam.
peso da mão mais peso do antebraço
no sentido horário. Perceba que a massa do braço (antebraço + mão) faz o corpo girar no sentido horário
De forma análoga, achamos
=
força que o tríceps faz para cima
De forma análoga, achamos
Peso do bloco
s 30°. Nesse caso o sentido é anti-horário. Perceba que o bloco faz o corpo girar no sentido anti-horário.
Agora, definindo o sentido anti-horário como positivo, montamos a equação:
Passo 2
Vamos analisar o sentido dessa força agora.
Definimos que o sentido anti-horário é positivo. Então:
Logo, percebemos que o sentido do momento gerado pelo força do tríceps é horário. Para ele ser horário, sua força tem que ser para cima.
Repare na figura abaixo como se orienta o sentido do giro quando a força do tríceps é para cima.
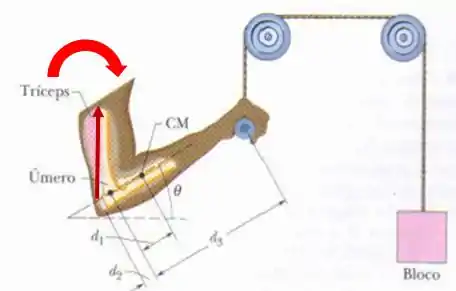
Passo 3
Agora, podemos aplicar outra condição para o equilíbrio estático para descobrir , ou seja, a força do úmero.
Logo, o módulo de é igual a
Passo 4
O sentido é encontrado pelo sinal que achamos acima. Como orientamos as forças para cima como positivas e as forças negativas para baixo, a força do úmero tem sentido para baixo.
Resposta
- Para cima
- Para baixo