Calcule as composições das fases (líquido-vapor) na mistura metano-monóxido de carbono a 100°C e 4MPa sabendo que o monóxido de carbono puro é um gás e que o metano puro é um líquido nesse estado. Admita o modelo de solução ideal nas duas fases. Dados:
- ; .
- ; .
- (monóxido de carbono como líquido hipotético)
- (metano como vapor hipotético)
Passo 1
Aqui é crucial perceber que nessa temperatura e pressão o monóxido de carbono é vapor enquanto o metano é líquido, por isso o problema forneceu uma fugacidade hipotética, pois eventualmente vamos utilizar a equação
Mesmo que não exista fase líquida ou vapor, existe uma fugacidade hipotética associada áquela situação.
Passo 2
Vamos achar as temperaturas relativas e pressões reduzidas para cada componente.
Passo 3
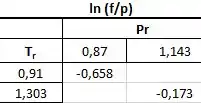
Utilizando a tabela fornecida no problema podemos calcular a fugacidade de cada componente (associadas às suas fases que realmente existem).
Para o metano:
Para o monóxido de carbono:
Passo 4
Utilizar as fugacidades calculadas e fornecidas para achar uma relação entre as composições das fases
Para o metano
Para o monóxido de carbono
Passo 5
Utilizar as relações
Para achar as composições das fases
Substituindo na primeira equação
Multiplicando a segunda por 0,4667 teremos
Subtraindo as duas
Portanto
E