Determine o erro em regime permanente para entradas de , e para o sistema mostrado abaixo. Sabendo que:
E que é o degrau unitário.
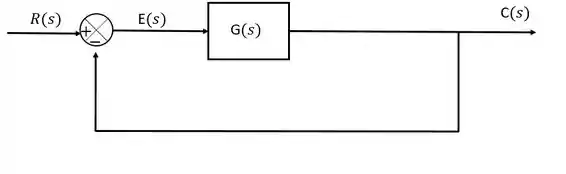
Passo 1
Pelo diagrama temos que:
E:
Substituindo a primeira na segunda:
Portanto:
Passo 2
Fazendo primeiramente para a entrada .
Substituindo o valor de que foi dado no enunciado e a entrada degrau, encontraremos a expressão do erro do sistema:
Rearranjando:
Aplicando o teorema do valor final:
Passo 3
Para a entrada :
Substituindo na expressão do erro:
Rearranjando:
E aplicando o teorema do valor final:
Passo 4
Por fim, para a entrada :
Então, a expressão de fica assim:
Rearranjando:
E aplicando o teorema do valor final:
Resposta
Para:
Esses resultados são coerentes visto que a função de transferência é do tipo 1.