Sabendo-se que a equação admite uma raiz no intervalo , determine o valor desta raiz usando interpolação quadrática. Estime o erro cometido, se possível.
Passo 1
Vamos começar montando uma tabela com alguns pontos:
![]()
O que vamos fazer agora é escrever como função de e não mais como função de . Ficamos com:
![]()
Assim nós não precisamos encontrar o zero do polinômio interpolador. Podemos jogar o zero direto no que vamos encontrar! Agora é só seguirmos o passo a passo de sempre ;)
Como ele quer uma função de interpolação quadrática, precisamos de pontos. Vamos usar , e . Além disso para estimarmos a incerteza precisamos de um quarto ponto para obtermos um operador diferenças divididas de ordem . Vamos usar então o . A tabela fica:
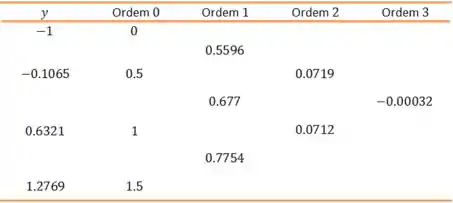
Passo 2
Da tabela tiramos que:
Substituindo no polinômio:
Substituindo ,
Passo 3
Agora para estimar o erro usamos a fórmula: