Defina a estabilidade do sistema representado pela malha feedback abaixo:
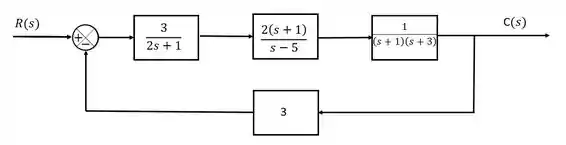
Passo 1
O primeiro passo, sempre que queremos determinar a estabilidade de uma malha, é encontrar a equação característica da malha. Para esse sistema, como estamos trabalhando com um feedback clássicozão, a função de transferência ficará assim:
Caso você tenha dúvidas em como obter essa expressão, dá uma revisadinha na aula de álgebra de diagrama de blocos.
Nós precisamos da equação característica, e ela sempre será o denominador da função de transferência. Então:
Passo 2
Vamos então deixar essa equação mais bonitinha pra gente poder pensar melhor sobre a estabilidade. Multiplicando toda a equação pelo denominador:
Fazendo as multiplicações:
Passo 3
Agora que já temos a nossa equação característica, poderíamos determinar a estabilidade dela pelo critério de Routh-Hurwitz. Entretanto, só de olhar pra carinha dela, já conseguimos ter um spoiler da nossa resposta.
O critério dos coeficientes diz que para o sistema ser estável, a sua equação característica precisa ter todos os sinais iguais.
Nesse caso, o critério não foi atendido. Portanto o sistema é instável.
Obs: só lembrando que esse critério é necessário, porém não suficiente.
Resposta
O sistema é instável de acordo com o critério dos coeficientes.