Determine se o sistema abaixo é estável: 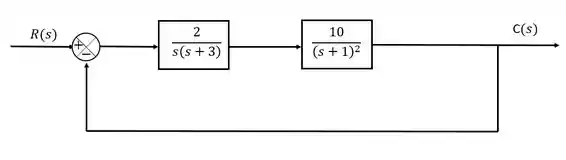
Passo 1
Primeiro precisamos definir nossa equação característica. Já vimos que para o feedback unitário, a equação característica fica da seguinte forma:
Onde e são os blocos do diagarama. Então:
Rearranjando:
Com a nossa equação característica em mãos, só precisamos aplicar o critério de Routh-Hurwitz para definir a estabilidade:
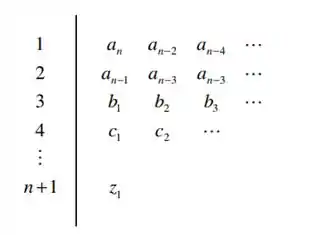
Passo 2
Vamos substituir os termos no diagrama então:
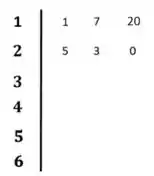
E vamos calcular os termos da terceira linha conforme as fórmulas:
Vamos colocar esses termos no diagrama:
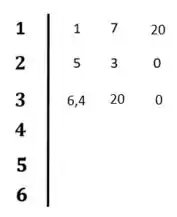
Passo 3
Vamos passar então para a quarta linha:
Então:

Passo 4
Para finalizar. Calculamos os coeficientes das duas últimas linhas:
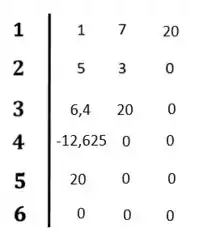
Completando nosso diagrama:
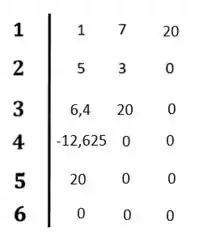
Resposta
O sistema é instável porque existe mudança de sinal na primeira coluna do diagrama de Routh-Hurwitz.