Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Estabilidade e critério de Routh-Hurwitz

Ver Teoria
Exercício 41235678

Enunciado

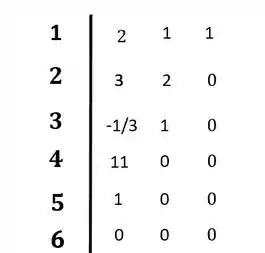
Determine se o sistema representado pela função de transferência abaixo é estável:

C s R s = 1 2 s 4 + 3 s 3 + s 2 + 2 s + 1

Passo 1

A nossa equação característica é:

2 s 4 + 3 s 3 + s 2 + 2 s + 1 = 0

E devemos montar nosso diagrama de Routh, seguindo o modelo para equação com 5 termos:

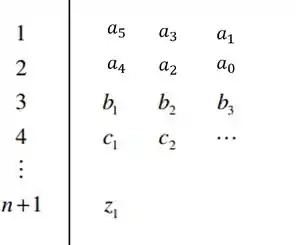
Passo 2

Primeiramente, vamos colocar os coeficientes da equação característica nas duas primeiras linhas:

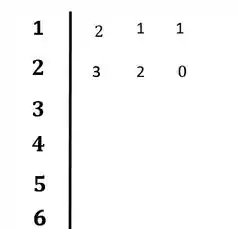
Passo 3

Vamos então calcular os faores da linha 3:

b 1 = a 4 a 3 - a 5 a 2 a 4 = 3 1 - 2 2 3 = - 1 3

b 2 = a 4 a 1 - a 5 a 0 a 4 = 3 1 - 2 0 3 = 1

b 3 = 0

Colocando no diagrama:

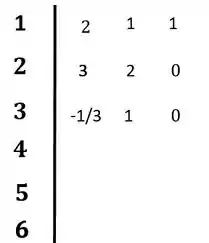
Passo 4

Calculando os fatores da quarta linha:

c 1 = b 1 a 2 - a 4 b 2 b 1 = - 1 3 2 - 3 1 - 1 3 = 11

c 2 = b 1 a 0 - a 4 b 3 b 1 = - 1 3 0 - 3 0 - 1 3 = 0

E os termos da quinta e sexta linha:

d 1 = 11 1 - - 1 3 0 11 = 1

d 2 = 0

e 1 = 0

Colocando no diagrama:

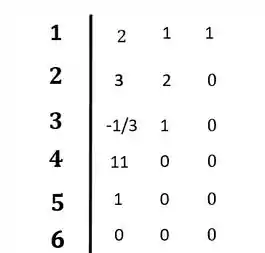
O sistema não é estável pois ocorreu mudança de sinal na primeira coluna do diagrama de Routh-Hurwitz.

Resposta

Sistema instável.