Determine a estabilidade da função de transferência em malha fechada:
Passo 1
O primeiro passo será determinar a nossa equação característica, como a função de transferência dada já é a da malha, a equação característica é:
Em seguida devemos utilizar o diagrama e Routh-Hurwitz para determinar a estabilidade do sistema:

Passo 2
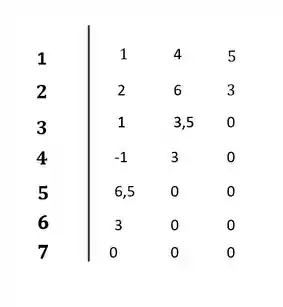
Vamos então dispor os coeficientes da equação característica nas duas primeiras linhas do diagrama de Routh-Hurwitz:

Passo 3
Em seguida, calculamos os coeficientes da linha 3:
Substtituindo os valores encontrados no diagrama:

Passo 4
Seguindo os cálculos agora, vamos para a linha 4:
Não precisamos calcular os próximos termos dessa linha, pois eles serão .
Colocando no diagrama:

Passo 5
Calculando as últimas linhas agora:
No diagrama:
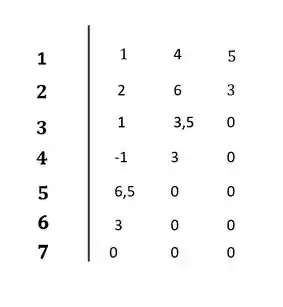
Sendo assim, o sistema é instável, pois apresenta duas mudanças de sinal na primeira coluna do diagrama, indicando a presença de duas raízes no semi-plano direito (parte real positiva).
Resposta
Sistema instável.