Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Estabilidade e critério de Routh-Hurwitz

Ver Teoria
Exercício 51234678

Enunciado

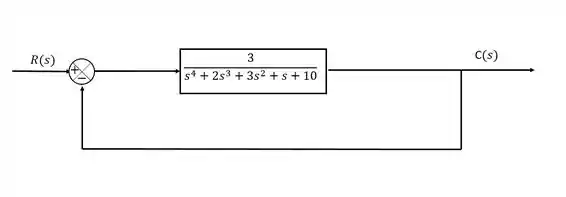
Determine se a malha abaixo é estável:

Passo 1

Primeiramente devemos definir nossa equação característica. Para isso, precisamos da função de transferência da malha:

C s R s = G s 1 + G s

Com G ( s ) sendo a função de transferência do bloco.

A nossa equação característica será então:

1 + G s = 0

1 + 3 s 4 + 2 s 3 + 3 s 2 + s + 10 = 0  

Rearranjando:

s 4 + 2 s 3 + 3 s 2 + s + 13 = 0

Agora que já temos nossa equação característica, precisamos aplicá-la no modelo abaixo para conseguir determinar a estabilidade da malha:

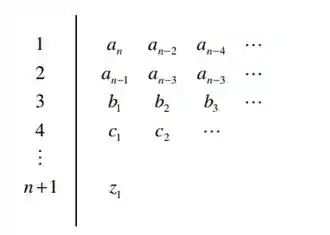
Passo 2

Vamos então, dispor os coeficientes da equação característica nas duas primeiras linhas:

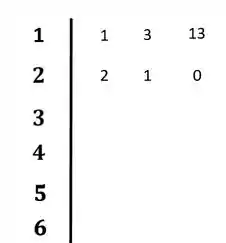
Vamos calcular agora os elementos da linha 3:

b 1 = a 3 a 2 - a 4 a 1 a 3 = 2 3 - 1 1 2 = 2,5

b 2 = a 3 a 0 - a 4 a - 1 a 3 = 2 13 - 1 0 2 = 13

b 3 = 0

Colocando no diagram:

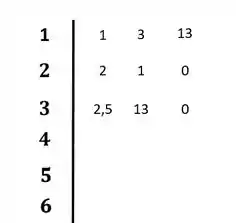
Passo 3

Calculando agora os elementos da terceira linha:

c 1 = b 1 a 1 - a 3 b 2 b 1 = 2,5 1 - 2 13 2,5 = - 9,4

c 2 = b 1 a - 1 - a 3 b 3 b 1 = 2,5 0 - 2 0 0 = 0

c 3 = 0

Passando para o diagrama:

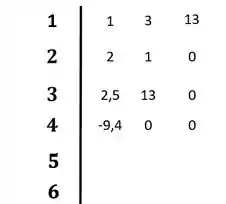
Passo 4

Agora para as duas últimas linhas:

d 1 = - 9,4 13 - 2,5 0 - 9,4 = 13  

d 2 = d 3 = 0

e 1 = 0

Completando o diagrama:

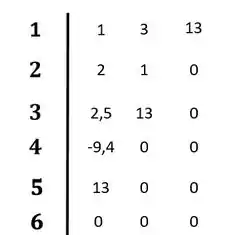
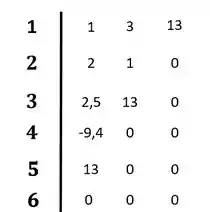
Resposta

O sistema é instável pois ocorre mudança de sinais na primeira coluna do diagrama de Routh-Hurwitz.