Teoria
Estabilidade
E aí? Tudo na paz, no equilíbrio? Bem, no tópico de Empuxo vimos como se dá o equilíbrio de um corpo flutuante. Mas esse equilíbrio é um equilíbrio estável, instável ou indiferente? Melhorando minha pergunta, quero saber se depois que o navio atingir o equilíbrio se uma força pequena for feita de lado o navio vai virar ou tender a voltar ao equilíbrio?

Antes de começarmos a estudar isso vamos relembrar os tipos de equilíbrios que acabei de citar e que serão mencionados nos exercícios e provas:

O equilíbrio estável é aquele que apesar de uma pequena variação de força o equilíbrio irá se recuperar quando a força for retirada. Já o instável é aquele equilíbrio que um pequeno movimento irá jogar o equilíbrio para o espaço. E o indiferente é aquele que vai achar uma outra posição de equilíbrio ali do lado.
Para se determinar se um objeto imerso em um fluido é estável ou não precisamos saber quanto vale a distância entre o metacentro e o centro de gravidade do objeto.
Essa distância será chamada de altura metacêntrica, . Então, foi descoberta a seguinte relação:
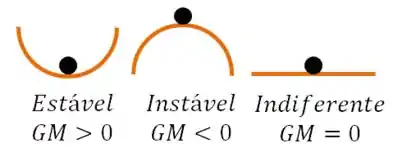
Então para um objeto estar estável o metacentro deve estar posicionado acima do centro de gravidade.
Mas que ponto é esse tal de metacentro?
É ponto de giro de um objeto flutuante, é como se ele girasse entorno daquele ponto. Ele é tão importante porque é ele que vai ajudar a definir se o objeto é estável ou não.
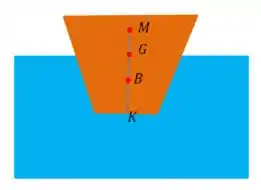
E como calculá-lo? Vamos calculá-lo em função do fundo do objeto o ponto . Se assumirmos que lá é o ponto zero, então teremos as cotas do centro de gravidade, empuxo e metacentro.
A equação para calcular a distância é simples: basta olhar para a imagem acima:
Ou
Opa apareceu o que a gente quer, no início falamos que o que vai definir se o objeto é estável ou não é a altura metacêntrica, o .
Se igualarmos as duas opções de , temos:
Isolando a altura metacêntrica, temos:
Beleza, que é a posição do centro de empuxo e que é a posição do centro de gravidade a gente sabe calcular. Só falta então descobrir quem é esse .
é chamado de raio metacêntrico, é a distância entre o centro de empuxo e o metacentro. E o cálculo dessa distância é relacionado com a forma do objeto, pois é:
é o momento de inércia da área onde objeto em contato com a superfície do fluido.
“Oi?? Não entendi nada!!” Calma, vamos desenhar, porque isso é foda. Faremos o momento de inércia dessa região aqui em preto:
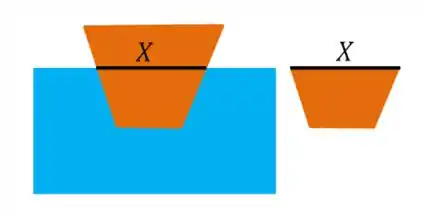
É a região que a água toca do objeto, olhando de cima, veríamos isso:
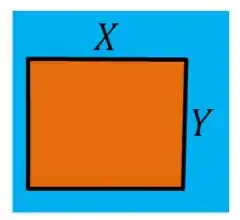
Onde seria o comprimento do nosso objeto analisado. Assim, o momento de inércia dessa região é:
Agora, conseguimos calcular o valor de e assim avaliar se o objeto está ou não estável. Partiu exercício?