Considere um tanque de água cilíndrico com área da base igual a e com um orifício de área no fundo, como mostra a figura abaixo. Se a velocidade da água através do orifício é conhecida e igual a e a altura inicial da água no tanque for , determine a altura da água como uma função do tempo .
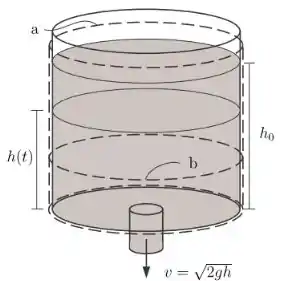
Passo 1
Vamos primeiro escolher o volume de controle. Nosso volume de controle será o tanque cilíndrico. Assim, podemos montar a equação para massa desse escoamento.
Como há conservação de massa então o primeiro termo é zero. E como não há entrada de fluido então o fluxo de entrada também é zero. Assim, só resta:
Como escolhemos um volume de controle fixo e com superfície de saída perpendicular ao escoamento, nosso ângulo será , afinal, esse é o ângulo entre o escoamento e o vetor normal da superfície (nesse caso, ambos apontam para baixo). Usamos então que:
E simplificamos para:
A velocidade foi dada e podemos considerar a densidade constante, então temos:
Vamos resolver as integrais. A primeira é simples é o próprio volume. E a segunda como a integral é em relação a área de saída, então a velocidade pode sair da integral e assim o resultado seria a área de saída. Resultando em:
Colocando o que é constante para fora da derivada temos:
Isolando os temos que tem de um lado, temos:
Integrando dos dois lados temos:
Agora substituindo os limites das integrais temos:
Elevando os dois lados ao quadrado temos: