Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Teorema de Transporte de Reynolds e Princípio da Continuidade

Ver Teoria
Exercício 1234567

Enunciado

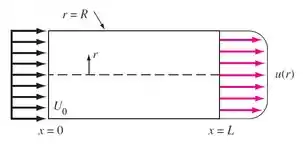
Água, admitida incompressível, escoa em regime permanente pelo tubo da figura. A velocidade na entrada é constante, u =   U 0 , e a velocidade na saída se aproxima do perfil para escoamento turbulento, u =   u m á x ( 1 - r R ) 1 / 7 . Determine a razão U 0 / u m á x para esse escoamento.

Passo 1

A primeira coisa que o enunciado nos diz é que o escoamento é incompressível e permanente.

Isso simplifica as coisas! Como o escoamento é permanente, d ρ d t = 0 .

Então, vimos na teoria que o princípio da continuidade (conservação da massa) para o caso permanente é:

∫ S C ρ . v r . c o s θ   d A s a i d a = ∫ S C ρ . v r . c o s θ   d A e n t r a d a

E, como o fluido é incompressível, ρ não varia e posso tirar ele da integral. Vou cortar porque ele está nos dois lados:

∫ S C v r . c o s θ   d A s a i d a = ∫ S C v r . c o s θ   d A e n t r a d a

O escoamento é todo na horizontal e faz 90° ( α ) com as superfícies de controle. Então, θ = 90 - α = 0 ° e cos ⁡ θ = 1

∫ S C v r   d A s a i d a = ∫ S C v r   d A e n t r a d a

v r são os perfis de velocidade. Vamos ver isso no passo 2!

Passo 2

O enunciado nos informou que a velocidade na entrada é constante e igual a U 0 , logo, podemos escrever assim:

∫ S C v r   d A e n t r a d a =   ∫ S C U 0   d A e n t r a d a =   U 0 ∫ S C   d A e n t r a d a

A área de entrada é a área A do tubo:

∫ S C v r   d A e n t r a d a = U 0   A =   U 0 π R ²

Por outro lado, na saída, o enunciado nos diz que a velocidade não é constante, mas segue esse perfil:

v s a í d a = u =   u m á x 1 - r R 1 / 7

Substituindo:

∫ S C v r   d A s a i d a =   ∫ S C u m á x 1 - r R 1 / 7   d A s a i d a

u m á x é a velocidade máxima, um valor constante e que sai da integral:

∫ S C v r   d A s a i d a =   u m á x ∫ S C 1 - r R 1 / 7   d A s a i d a

Vamos ter que resolver essa integral aí? Relaxa, vamos conseguir e estamos aqui para isso! Vamos resolvê-la passo a passo!

Passo 3

Resolvendo a Integral

Primeiro, quem é esse d A s a i d a ? Repara que quem está dentro dessa integral depende de r. Além disso, a área de saída é a área de um círculo, então podemos escrever assim:

d A s a i d a = 2 π . r . d r

E a integral fica assim:

∫ S C v r   d A s a i d a =   u m á x ∫ 0 R 1 - r R 1 / 7   2 π . r . d r

∫ S C v r   d A s a i d a =   2 π . u m á x ∫ 0 R 1 - r R 1 / 7   r . d r

Outra coisa importante: aquele 1/7 está elevando 1 - r R todo. Então, não vai dar para separar 1 e r/R tão fácil. Vamos usar a integral por substituição:

u =   1 - r R

A partir daí achamos d u :

d u =   - 1 R d r   ⇒ d r =   - R d u

Reorganizando u =   1 - r R :

r R = 1 - u   ⇒ r = R ( 1 - u )

Antes de substituir, precisamos atualizar nossos limites

r = 0   ⇒ u = 1 r = R   ⇒ u = 0

Substituindo, nossa integral vai ficar:

2 π . u m á x ∫ 0 R 1 - r R 1 / 7   r . d r

2 π . u m á x ∫ 1 0 u 1 7 .   R 1 - u . ( - R d u )

Vamos arrumar isso aí colocando as constantes para fora:

- 2 π R ² . u m á x ∫ 1 0 u 1 7 .   1 - u . d u

Consertando os limites:

2 π R ² . u m á x ∫ 0 1 u 1 7 .   1 - u . d u

Fazendo a distributiva:

2 π R 2 . u m á x ∫ 0 1 u 1 7 - u 8 7   d u

Separando as integrais:

2 π R 2 . u m á x ∫ 0 1 u 1 7 d u -   ∫ 0 1 u 8 7 d u

Agora é nosso momento! Vamos integrar!

2 π R 2 . u m á x u 8 7 8 / 7 0 1 - u 15 7 15 / 7 0 1

2 π R 2 . u m á x 7 u 8 / 7 8 0 1 - 7 u 15 / 7 15 0 1

Fazendo as contas:

2 π R 2 . u m á x 7 8 . 1 - 7 15 . 1 ⇒ 2 π R 2 . u m á x 7 8 - 7 15

2 π . 7 . R 2 . u m á x 1 8 - 1 15 ⇒ 2 π . 7 . R 2 . u m á x 15 - 8 8.15

2 π . 7 . R 2 . u m á x 7 8.15 ⇒ π . R 2 . 7 2 .   u m á x 60  

E essa integral que a gente está calculando era quem mesmo?

∫ S C v r   d A s a i d a =   π . R 2 . 7 2 .   u m á x 60

Opa! Encontramos uma expressão para essa integral, que faz parte do princípio da continuidade. Aliás, falando nele, vamos lembrar?

Passo 4

Princípio da continuidade para escoamento incompressível e permanente (vimos no passo 1)

∫ S C v r   d A s a i d a = ∫ S C v r   d A e n t r a d a

E nos passo 2 e 3, calculamos essas 2 integrais. Substituindo:

U 0 π R 2 =   π . R 2 . 7 2 .   u m á x 60

Cancelando π R 2

U 0 =   49   u m á x 60

Estamos quase lá!!

U 0 u m á x =   49   60

UHUL! Encontraaaamos a razão U 0 / u m á x para esse escoamento.

Resposta

U 0 u m á x =   49   60

Exercícios de Livros Relacionados

A distribuição de velocidades para escoamento laminar em um longo tubo circular de raio R é dada pela expressão unidimensional, V → = u i ^ = u m a x 1 - r R 2 i ^ Para este perfil, obtenha expressões
Uma curva redutora bidimensional tem um perfil de velocidade linear na seção 1 . O escoamento é uniforme nas seções 2 e 3 . O fluido é incompressível e o escoamento é permanente. Determine o módulo e
No tubo em U da figura, de seção de área A, oscila, em torna da posição de equilíbrio, uma coluna de comprimento total L de um líquido admitido ideal. Determinar o período T da oscilação.
A massa de gás no interior de um botijão varia segundo a lei: m t = m 0 - β t , onde β = c t e . Sendo ρ s a massa específica do gás na seção de saída, calcular a velocidade média nessa seção, cuja ár
Na instalação, a vazão de 100 L/s divide-se igualmente nos dois ramais. Qual é o momento em relação ao eixo z devido somente à ação da água? Dados: A 2 = A 3 = 2 ⋅ 10 - 3m 2 ; p 1 = 100P a ; γ = 10 4N