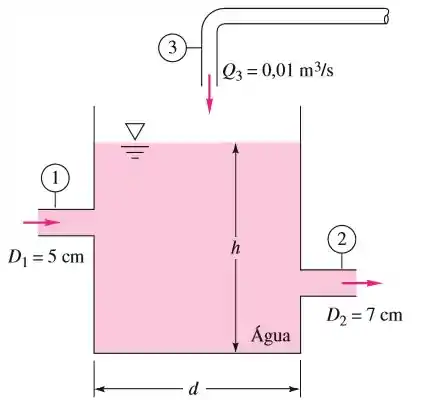
O tanque aberto da figura abaixo contém água a e está sendo enchido através da seção . Considere o escoamento incompressível. Primeiro, deduza uma expressão analítica para a taxa de variação do nível d’água, , em termos das vazões e do diâmetro do tanque , arbitrários. Em seguida, se o nível d’água for constante, determine a velocidade na saída, para os dados e .

Queremos saber a variação de altura do fluido dado a entrada e saída de fluidos. Para isso vamos analisar a massa do sistema, sabendo que haverá uma conservação de massa, assim se o que entra não é igual ao que sai, essa massa sobrando deve ocupar algum espaço. E será isso que fará varia.

Então vamos montar a equação:

Como a massa do sistema vai se conservar então:

Porém a massa do volume de controle irá variar se o fluxo de entrada for diferente do fluxo de saída. Assim, temos:

Isso era para um volume de controle qualquer, mas agora, vamos escolher nosso volume de controle de forma a nos ajudar.

Ele será fixo, tanto na forma quanto na posição. Assim, vira , e poderemos escrever como vazão o termo: .

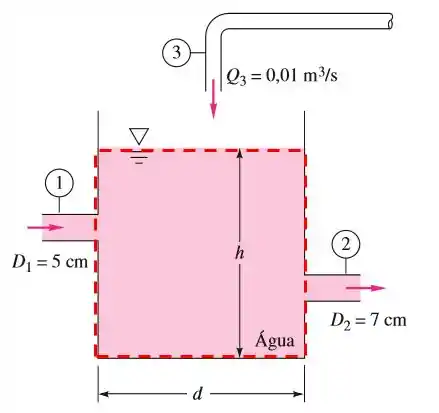
Nosso volume de controle é um paralelepípedo, que terá três superfícies onde haverá fluxo de fluido. As superfícies são as partes que cortam a região .

Vamos reescrever a equação agora colocando em função das vazões:

Podemos colocar a densidade para fora da integral, e a integral do volume de controle será o volume do paralelepípedo, que é

Como só a altura irá variar, então temos:

Cortando a densidade dos dois lados e vendo que o enunciado falou que e são entradas de fluido e é saída, temos:

Chegamos na primeira resposta.