Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 5.Problemas - Ex. 50
5.50 Como uma das etapas de um estudo sobre poluição, um modelo de concentração em função da posição foi desenvolvido, em que a concentração é dada por , em que (parte por milhão) e . Trace o gráfico desta concentração desde até . Se um veículo com um sensor de poluição viaja através desta atmosfera a , desenvolva uma expressão para a taxa de concentração medida de mudança de com o tempo, e trace um gráfico usando esses dados.
(a) Em qual localização o sensor indicará a maior taxa de mudança?
(b) Qual é o valor dessa taxa de mudança?
Passo 1
O gráfico desta concentração (usando o Geogebra):
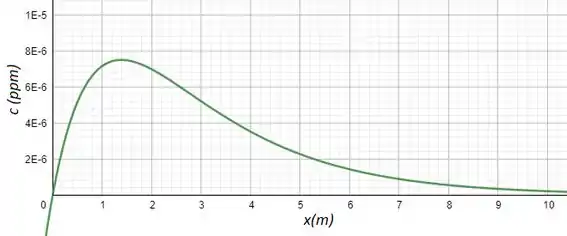
Passo 2
Considerando que só há variação da concentração em x, Vamos usar derivada substantiva para achar a taxa:
Mas a variação tem que ser com tempo e não com x. Podemos escrever:
Então:
O gráfico da taxa:
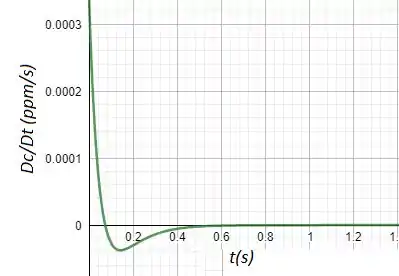
Passo 3
(a) Aqui nós temos um probleminha com o que ele pede. Como dá pra ver no gráfico da taxa, não tem um ponto de máximo, mas um ponto de mínimo. Se a gente derivar a taxa e igualar a zero, nós não vamos achar a taxa máxima, mas sim a mínima. Mas é razoável ver quer a taxa máxima é em e nesse caso o também seria zero.
Faria mais sentido perguntar onde é a concentração máxima (o gráfico da conentração tem um ponto de máximo). Vamos calcular qual é esse ponto de máximo e onde é.
Como ,
Se formos olhar no gráfico de concentração faz bastante sentido.
(b) O valor dessa concentração é:
Resposta
(a)
(b)