Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 5.Problemas - Ex. 66
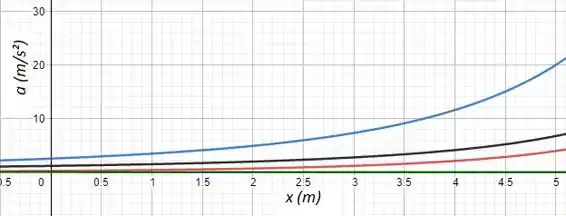
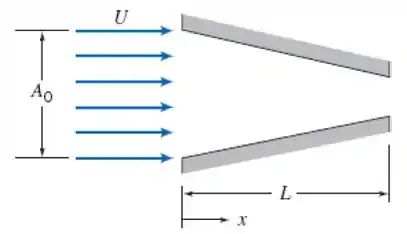
5.66 Considere o escoamento incompressível de um fluido através de um bocal, conforme mostrado. A área do bocal é dada por e a velocidade de entrada varia de acordo com , em que , , , e . Determine e trace um gráfico da aceleração na linha central, usando o tempo como parâmetro.
Passo 1
Usando a equação da continuidade para achar uma expressão para a velocidade na linha central,
Passo 2
Como só tem variação em x e em t, podemos calcular a aceleração por:
Vamos calcular as derivadas parciais:
Então:
Passo 3
Usando o tempo como parâmetro:
Com : (azul)
Com (vermelho)
Com : (verde)
Com : (preto)
Resposta
Exercícios de Livros Relacionados
Óleo, de massa específica ρ e viscosidade μ , é drenado continuamente por um lado de uma placa vertical, como na Figura P4.80. Após uma região de desenvolvimento próximo ao topo da placa, o filme de ó
Um cilindro sólido longo gira em regime permanente em um fluido muito viscoso, como mostrado abaixo. Considerando escoamento laminar, resolva a equação de Navier-Stokes em coordenadas cilíndricas para
Considere o escoamento de Couette bidimensional, incompressível e permanente (escoamento entre duas placas infinitas com a placa superior se movendo a uma velocidade constante, e a inferior estacionár
Uma correi move-se para cima com a velocidade V, arrastando um filme de líquido viscoso de espessura h, como mostrado abaixo. Próximo à correia, o filme move-se para cima em virtude da condição de não
Para a distribuição de velocidade do Problema P4.4, determine se são satisfeitas (a) a equação da continuidade e (b) a equação de Navier-Stokes. (c) Se essa última afirmação for verdadeira, encontre a