Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 5.Problemas - Ex. 83

5.83 Considere o escoamento representado pelo campo de velocidade V → = A y + B i ^ + A x j ^ , em que A = 10   s - 1 , B = 3   m - 1 s - 1 e as coordenadas são medidas em metros.

(a) Obtenha uma expressão para a função de corrente.

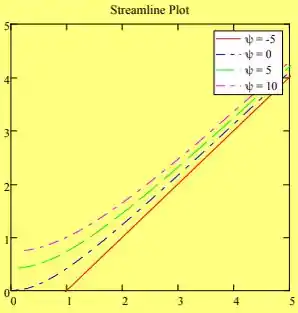
(b) Trace algumas linhas de corrente (incluindo a linha de corrente de estagnação) no primeiro quadrante.

(c) Avalie a circulação sobre a “curva” delimitada por y=0, x=1, y=1 e x=0

Passo 1

(a) Da definição de função de corrente,

u = ∂ ψ ∂ y

A y + B = ∂ ψ ∂ y

Separando as variáveis e integrando,

d ψ = A y + B d y

∫ d ψ = ∫ A y + B d y

ψ = A y 2 2 + B y + C

Onde C é constante de integração.

Também da definição de função de corrente,

v = - ∂ ψ ∂ x

A x = - ∂ ψ ∂ x

Separando as variáveis e integrando,

d ψ = - A x d x

∫ d ψ = ∫ - A x d x

ψ = - A x 2 2 + K

Onde K é constante de integração.

Comparando as duas, ficamos com:

C = - A x 2 2

K = A y 2 2 + B y

Então:

ψ = A y 2 2 + B y - A x 2 2

ψ = A 2 y 2 - x 2 + B y

ψ = 5 y 2 - x 2 + 3 y

Passo 2

(b) Para as linhas de corrente é só fazer ψ constante.

A linha de corrente de estagnação é quando a velocidade é igual a zero, então:

Em u=0:

10 y e s t + 3 = 0

y e s t = - 0,3   m

Em v=0

10 x e s t = 0

x e s t = 0

Portanto,

ψ = 5 y e s t 2 - x e s t 2 + 3 y e s t

ψ = 5 - 0,3 2 - 0 2 + 3 - 0,3

ψ = - 0,45   ~ - 0,5   m 2 / s  

Passo 3

(c) Da definição de circulação:

Γ = ∮ V → ⋅ d S

Graças ao bom deus podemos representar essa integral por: (por serem retas na vertical e na horizontal e bla bla bla)

Γ = ∫ x a x b u   d x + ∫ y b y c v   d y + ∫ x c x d u   d x + ∫ y d y a v   d x

Como u = A y + B e v = A x

Γ = ∫ a b A y + B     d x + ∫ b c A x   d y + ∫ c d A y + B     d x + ∫ d a A x   d x

Γ = A y - B x a b + A x y b c + A y - B x c d + A x y d a

Como os pontos são a = 0,0 , b = 1,0 , c = 1,1 e d = 0,1 ,

Γ = 0

Resposta

(a) ψ = 5 y 2 - x 2 + 3 y

(c) Γ = 0

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Mostre que a equação da continuidade incompressível para escoamento axissimétrico em coordenadas polares esféricas, 1 r∂ ∂ r r 2 u r + 1 sin ⁡ θ ∂ ∂ θ u θ sin ⁡ θ = 0 , é de forma idêntica, satisfeita
A função de corrente para o escoamento bidimensional permanente, incompressível sobre um cilindro circular de raio a e velocidade da corrente livre V ∞ é ψ = V ∞ sin ⁡ θ r - a 2 r para ocaso no qual o
Considere uma linha de vórtice irrotacional de intensidade Γ no plano x y ou r θ . As componentes da velocidade são: u r = ∂ ϕ ∂ r = 1 r ∂ ψ ∂ θ = 0 e u θ = 1 r ∂ ϕ ∂ θ = - ∂ ψ ∂ r = Γ 2 π r Gere expr
Considere uma corrente uniforme de intensidade V inclinada com um ângulo a (Figura P 10 - 56 ). Supondo escoamento irrotacional incompressível planar, determine a função potencial de velocidade e a fu
Considere uma linha de fonte irrotacional de intensidade V ˙ / L no plano x y ou r θ . As componentes da velocidade são: u r = ∂ ϕ ∂ r = 1 r ∂ ψ ∂ θ = V ˙ / L2 π r e u θ = 1 r ∂ ϕ ∂ θ = - ∂ ψ ∂ r = 0