Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 5.Problemas - Ex. 58

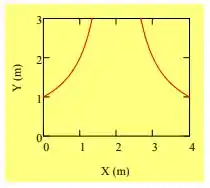
5.58 Um campo de velocidade é dado por V → = A x - B i ^ + C y j ^ + D t k ^ , em que A = 2   s - 1 , B = 4   m   s - 1 , D = 5   m   s - 2 e as coordenadas são medidas em metros. Determine o valor próprio para C se o escoamento é incompressível. Calcule a aceleração de uma partícula fluida localizada no ponto (x,y)=(3,2). Esboce algumas linhas de corrente do escoamento no plano xy.

Passo 1

Vamos começar pela equação da continuidade

∂ ρ u ∂ x + ∂ ρ v ∂ y + ∂ ρ w ∂ z + ∂ ρ ∂ t = 0

Para incompressível, podemos tirar o ρ de dentro da derivada e ∂ ρ ∂ t = 0

ρ ∂ u ∂ x + ∂ v ∂ y + ∂ w ∂ z = 0

Simplificando, ficamos com

∂ u ∂ x + ∂ v ∂ y + ∂ w ∂ z = 0

Como u = A x - B , v = C y e w = D t

∂ A x - B ∂ x + ∂ C y ∂ y + ∂ D t ∂ z = 0

A + C + 0 = 0

C = - A

Como A = 2   s - 1

C = - 2   s - 1

Passo 2

Para a aceleração da partícula

a → p = u ∂ V → ∂ x + v ∂ V → ∂ y + w ∂ V → ∂ z + ∂ V → ∂ t

Calculando as derivadas parciais primeiro

∂ V → ∂ x = A   i ^

∂ V → ∂ y = C   j ^

∂ V → ∂ z = 0

∂ V → ∂ t = D   k ^

Substituindo

a → p = A x - B A   i ^ + C y C   j ^ + D t 0 + D   k ^

a → p = A 2 x - A B i ^ + C 2 y j ^ + 0 + D   k ^

a → p = A 2 x - A B i ^ + C 2 y j ^ + D   k ^

No ponto x , y = 3,2

a → p 3,2 = A 2 3 - A B i ^ + C 2 2 j ^ + D   k ^

a → p 3,2 = 3 A 2 - A B i ^ + 2 C 2 j ^ + D   k ^

Com A = 2   s - 1 , B = 4   m   s - 1 ,   C = - 2   s - 1 e D = 5   m   s - 2

a → p 3,2 = 3 2 2 - 2 4 i ^ + 2 - 2 2 j ^ + 5   k ^

a → p 3,2 = 4 i ^ + 8 j ^ + 5   k ^

Passo 3

Pela definição de linhas de corrente

d y d x = v u

d y d x = C y A x - B

Separando as variáveis e integrando

d y C y = d x A x - B

∫ d y C y = ∫ d x A x - B

1 C ln ⁡ y = 1 A ln ⁡ A x - B + K

Onde K é constante.

Como C = - A , podemos escrever

- 1 A ln ⁡ y = 1 A ln ⁡ A x - B + K

Manipulando matemáticamente

1 A ln ⁡ A x - B + 1 A ln ⁡ y = - K

1 A ln ⁡ y A x - B = - K

ln ⁡ y A x - B = - K A

y A x - B = e - K A

Chamando K f = e - K A

y A x - B = K f

Resposta

C = - 2   s - 1

a → p 3,2 = 4 i ^ + 8 j ^ + 5   k ^

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

5.79 Considere o campo de escoamento representado pela função de corrente ψ = - A / 2 x 2 + y 2 , em que A é constante. Esse é um possível escoamento bidimensional incompressível? O escoamento é irrot
5.78 Considere um campo de velocidade para um movimento paralelo ao eixo x com cisalhamento constante. A taxa de cisalhamento é du/dy=A, em que A = 0,1s - 1 . Obtenha uma expressão para o campo de vel
5.77 Considere o campo de escoamento representado pela função de corrente ψ = x 6 - 15 x 4 y 2 + 15 x 2 y 4 - y 6 . Esse é um possível escoamento bidimensional incompressível? O escoamento é irrotacio
5.80 Considere o campo de escoamento representado pela função de corrente ψ = A x y + A y 2 , em que A = 1s - 1 . Mostre que este campo de velocidade representa um possível escoamento incompressível.
5.82 Considere o campo de velocidade dado por V → = A x 2 i ^ + B x y j ^ , em que A = 3,3m - 1 s - 1 , B = - 6,6m - 1 s - 1 e as coordenadas são medidas em ft.(a) Determine a rotação do fluido.(b) Av