5.64 O campo de velocidade para um escoamento permanente e não viscoso, da esquerda para a direita sobre um cilindro circular de raio R, é dado por V → = U cos ⁡ θ 1 - R r 2 e ^ r - Us e nθ1 + R r 2 e ^ θ . Obtenha expressões para a aceleração de uma partícula fluida movendo ao longo da linha de corrente de estagnação θ = π e para a aceleração ao longo da superfície do cilindro (r=R). Trace um gráfico de a r como uma função de r/R para θ = π , e outro de a r como função de θ para r=R; trace um gráfico de a θ como função de θ para r=R. Comente sobre os gráficos. Determine os locais em que estas acelerações atingem valores máximo e mínimo.

a p r = 2 U 2 R 2 r 3 1 - R r 2 a p θ = 0 a p r = - 4 U 2s e nθ 2 r a p θ = 4 U 2 s e nθ cos ⁡ θ r

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 5.Problemas - Ex. 64

5.64 O campo de velocidade para um escoamento permanente e não viscoso, da esquerda para a direita sobre um cilindro circular de raio R, é dado por . Obtenha expressões para a aceleração de uma partícula fluida movendo ao longo da linha de corrente de estagnação e para a aceleração ao longo da superfície do cilindro (r=R). Trace um gráfico de como uma função de r/R para , e outro de como função de para r=R; trace um gráfico de como função de para r=R. Comente sobre os gráficos. Determine os locais em que estas acelerações atingem valores máximo e mínimo.

Passo 1

Vamos considerar estado estacionário, fluido incompressível e, como a velocidade não é dependente, de z, não há componente z.

Para a aceleração a partir dessas considerações e em coordenadas cilíndricas, vamos já calcular as componente:

Passo 2

Primeiro vamos calcular para :

Então temos:

Calculando as derivadas parciais:

Portanto, as componentes da aceleração ficam:

Pelo gráfico podemos dizer que atinge valor máximo em .

Passo 3

Agora vamos calcular para :

Então temos:

Calculando as derivadas parciais:

Portanto, as componentes da aceleração ficam:

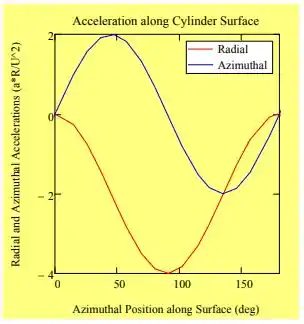
Pelo gráfico podemos dizer que tem valor máximo em e e valor mínimo em . (esses valores são bem razoáveis de serem vistos porque a função é seno, ne... seno é positiva de zero a 180 graus mesmo, mas tem um menos na frente bla bla bla)

Já para tem valor máximo em e valor mínimo em .

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

5.41 A componente x da velocidade em um campo de escoamento em regime permanente, incompressível, no plano x y , é u = A x 5 - 10 x 3 y 2 + 5 x y 4 , em que A = 2m - 4 s - 1 e x é medido em metros. En

5.44 A componente y da velocidade em um campo de escoamento bidimensional incompressível é dada por v = - A x y , em que v é em m / s , x e y são em metros e A é uma constante dimensional. Não há comp

5.56 Um campo de velocidade bidimensional permanente é dado por V → = A x i ^ - A y j ^ , em que A = 1s - 1 . Mostre que as linhas de corrente para este escoamento são hipérboles retangulares, x y = C

5.48 Considere o escoamento de ar de baixa velocidade entre dois discos paralelos, conforme mostrado. Suponha que o escoamento é incompressível e não viscoso e que a velocidade é puramente radial e un

5.72 Considere o campo de velocidade para escoamento em um “canto”, V → = A x i ^ - A y j ^ , com A = 0,3s - 1 , como no Exemplo 5.8. Avalie a circulação sobre o quadrado unitário do Exemplo 5.8.