94 – A função Der(T,t) de IHT pode ser usada para representar a derivada temperatura-tempo da equação 5.75. Neste problema nós usaremos a função Der para resolver o Exemplo 5.12.
(A) Mostre, usando o método do balanço de energia, que a forma implícita das equações de diferenças finitas para nodos 1≤m≤8 do exemplo 5.12 pode ser escrito como
Nota: IHT faz uso do esquema das diferenças finitas implícito.
(B) Derive a forma implícita da equação de diferenças finitas para nodo m=0 do Exemplo 5.12.
(C) Para T9=20°C e usando um intervalo de tempo de Δt=24 s, determine as temperaturas do nodo 0 até 8 em t=120 s.
Passo 1
A função Der(T,t) de IHT é um código computacional para solucionar problemas de transferência de calor em condições de regime transiente (variação com o tempo) usando os métodos de diferenças finitas. Você pode utilizar este código pesquisando em referências bibliográficas o seu funcionamento e em quais softwares aplica-lo.
Passo 2
(A)
Vamos iniciar esse item relembrando como funciona o método do balanço de energia que consiste em aplicar um balanço de energia ao redor de cada nodo para conseguir determinar a expressão que representará as temperaturas naquele nodo. A expressão geral usada é a seguinte:
Onde,
-, é taxa de transferência de energia que entra no sistema;
-, é a taxa de geração de energia dentro do sistema;
-, é taxa de energia acumulada no sistema, que varia com o tempo em um processo transiente.
A energia acumulada no sistema, lembrando, pode ser escrita da seguinte forma:
Então, com a Eq1 conseguimos determinar uma expressão para a temperatura em cada nodo.
Passo 3
Voltando ao Exemplo 5.12 do Incropera, temos que os nodos de 1 a 8, representam aqueles sem estar na superfície exposta do material. Os nodos das duas superfícies expostas do material são o nodo 0 e o nodo 9. Assim nestes nodos de 1 a 8, teremos apenas condução ocorrendo como energia de entrada no sistema, assim o termo de energia que entra no sistema da Eq1 será referente a taxa de transferência de calor por condução, qCond
Lembrando da equação do calor que a taxa de transferência de calor pode ser escrita em termos da variação de temperatura em relação a x:
Também pelo exemplo 5.12, temos que não há geração de energia, que a condução é unidimensional na direção de x e as propriedades são constantes, assim podemos escrever a Eq1 da seguinte forma:
Passo 4
Vamos agora discretizar a Eq2, isto é, transformar as derivadas da Eq2 em formas de diferenças finitas. Vamos usar o método implícito como sugerido no enunciado.
Relembrando do método de diferenças finitas implícito, temos que para uma derivada de segunda ordem a discretização desta é a seguinte:
Onde,
-o índice m é um nodo qualquer de número m, por exemplo m poderia ser m=1;
-Δx é o incremento espacial;
-p representa a posição temporal da temperatura, por exemplo, p poderia ser o tempo de nº 2, onde p e o tempo t são relacionados pela seguinte expressão:
Onde, Δt é o intervalo de tempo.
A discretização de uma derivada de primeira ordem para uma diferença finita implícita é
Mas, para este exercício, foi dito que a função Der(T, t) representa a derivada T-t na forma implícita de diferenças finitas, assim
Passo 5
Substituindo essas relações na Eq2:
Para chegarmos exatamente na expressão do enunciado, vamos fazer alguns algebrismos
Assim,
Portanto, foi demonstrado a expressão do enunciado.
Passo 6
(B)
Pelo exemplo 5.12, em nodo m=0 temos que neste nodo, onde é uma superfície exposta há um fluxo de calor por radiação q”0=3x105 W/m2. Assim pelo balanço de energia teremos que
Onde, V é o volume que é dado por
Pela Lei de Fourier, você pode expressar a taxa de transferência por condução assim
Assim,
Aplicando diferença finita de forma implícita nas derivadas:
Que podemos escrever também como:
Onde,
Substituindo os valores das propriedades dadas no exemplo 5.12, vamos chegar que:
Passo 7
(C)
Para este item podemos usar a eq. 5.97 do Incropera que é aplicada para nodos interiores com o método de diferenças finitas implícito. Assim, para os nodos de 1 até 8:
O número de Fourier, FO, deve seguir o critério de estabilidade, assim
Substituindo, vamos chegar que:
Essa é eq. para cada nodo m interior de 1 até 8
Passo 8
Assim, vamos ter que resolver o seguinte sistema linear:
...
Vamos considerar que no passo de tempo de p = 0, isto é, no tempo inicial, todas as temperaturas são iguais a 20ºC
Como temos um passo de tempo de 24 s, e precisamos encontrar as temperaturas para t = 120 s, então teremos que resolver o sistema linear 5 vezes.
Passo 9
Resolvendo pelo EXCEL, vamos chegar que as temperaturas de nodos 0 até 8, no tempo t = 120s são:
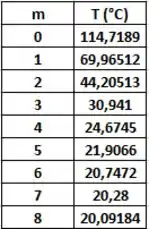
Resposta
A)
B)
C)