Para escoamento incompressível laminar totalmente desenvolvido através de um duto retilíneo de seção não circular, como na seção 6.8, as equações de Navier-Stokes (4.38) se reduzem a
em que (y,z) é o plano da seção transversal do duto e x é a coordenada do eixo do duto. A gravidade foi desprezada. Usando uma malha retangular não quadrada , desenvolva um modelo de diferenças finitias para essa equação e indique como ele pode ser aplicado para calcular o escoamento num duto retangular de lados e .
Passo 1
E aí, gente!! Tudo bem? Então vou mostrar pra vocês que mecânica dos fluidos não é nem de longe um bicho de 7 cabeças (nem de perto também)!
Primeira coisa que vamos fazer é desenhar nossa malha para obtermos os resultados por diferenças finitas, beleza?
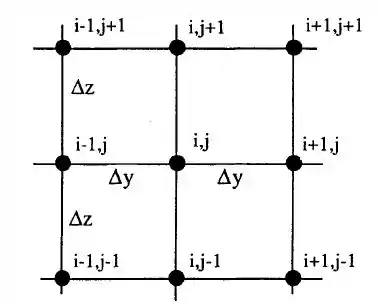
Passo 2
Portanto para esse modelo, podemos aplicar nossas diferenças finitas e termos a seguinte equação algébrica:
Passo 3
Mas se dizermos que
Note que isso é a nossa velha e antiga equação de Poisson!!!! Isso parece com o modelo de Laplace somado um termo fonte constante que envolve o tamanho da malha , o gradiente de pressão e viscosidade!!!