Enunciado
Cálculo Numérico - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 8º - Capítulo 5.Problemas - Ex. 113
113 – Uma chaminé passando gases quentes de exaustão tem uma área de seção transversal quadrada de 300 mm de lado. As paredes são construídas de tijolos refratários de 150 mm de espessura com uma condutividade térmica de 0,85 W/m.K e difusividade térmica α = 5,5x10-7m2/s. Inicialmente sem gases na chaminé escoando, as paredes estão a uma temperatura uniforme de 25°C. A superfície interior é rapidamente exposta aos gases quentes a 350°C com um coeficiente convecção de 100W/m2.K, enquanto a superfície exterior experimenta uma convecção com ar a 25°C e com coeficiente convectivo de 5W/m2.K. Usando um método de diferenças finitas implícito com um espaçamento de 50 mm e incremento de tempo de 1 h, encontre a distribuição de temperatura na parede e a taxa de perda de calor por convecção do exterior da chaminé em 5, 10, 50 e 100 h depois da introdução dos gases na chaminé.
Passo 1
Vamos começar determinando a expressão para a temperatura que representará a distribuição de temperatura.
Vamos fazer um balanço de energia na parede da chaminé.
O balanço de energia global é:
Onde,
- e , são, respectivamente, a taxa de transferência de energia que entra no sistema e a que sai do sistema;
-, é a taxa de geração de energia dentro do sistema;
-, é taxa de energia acumulada no sistema, que varia com o tempo em um processo transiente.
A energia acumulada no sistema é:
Desprezando a geração de energia:
A energia que entra no sistema é dada por:
E, a energia que sai é:
Passo 2
Assim, a Eq. 1 fica:
Onde,
Assim,
Passo 3
Aplicando diferenças finitas pele método implícito:
Assim, para o interior da parede:
Esse é o balanço de energia global na chaminé discretizado com diferenças finitas pelo método implícito.
Passo 4
Na superfície interna:
Onde,
Assim,
Onde, para p = 0:
Assim, aplicando os valores:
Passo 5
Na superfície externa:
Onde,
Assim,
Onde, para p = 0:
O nodo N é o nodo de nº 4.
Assim, aplicando os valores:
Assim,
Passo 6
Agora para os nodos interiores, podemos usar a Eq. 5.97 do Incropera que é aplicada para nodos interiores com o método de diferenças finitas implícito. Assim, para os nodos de 1 até 3:
Onde, FO é o nº de Fourier:
Substituindo, vamos chegar que:
Essa é eq. para cada nodo m interior de 1 até 3,
Passo 7
Vamos agora montar o sistema linear que compõem as equações para cada nodo:
Onde, no passo de tempo de p = 0, isto é, no tempo inicial, todas as temperaturas são iguais a 25ºC:
Passo 8
Resolvendo o sistema linear pelo EXCEL, obtemos a seguinte distribuição de temperatura na parede:
Para t = 5 h:
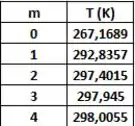
Para t = 10 h:
Resposta
Para t = 5 h:
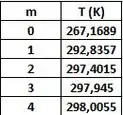
Para t = 10 h:
