Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 4.Problemas - Ex. 43

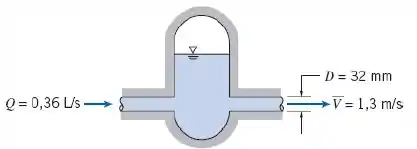
Um acumulador hidráulico é projetado para reduzir as pulsações de pressão do sistema hidráulico de uma máquina operatriz. Para o instante mostrado, determine a taxa à qual o acumulador ganha ou perde óleo hidráulico.

Passo 1

Dados fornecidos:

A vazão é Q = 0,36 L s = 0,00036 m 3 / s  

A velocidade do fluxo na saída é V 2 = 1,3   m / s  

O diâmetro do tubo na saída é D 2 = 32   m m = 0,032   m  

Passo 2

Podemos aplicar a equação da conservação de massa ao volume de controle. Assim obtemos que:

∂ ∂ t ∫ C V   ρ d ∀ + ∫ C S   ρ V → ⋅ d A → = 0

Queremos determine a taxa à qual o acumulador ganha ou perde óleo hidráulico, ou seja:

∂ ∂ t ∫ C V   ρ d ∀

Que pode ser excito como:

∂ ∂ t M V C

Assim, podemos reescrever a equação da conservação de massa da seguinte maneira:

∂ ∂ t M V C - ∫ A 1   ρ V 1 d A 1 + ∫ A 2   ρ V 2 d A 2 = 0

∂ ∂ t M V C - ρ V 1 A 1 + ρ V 2 A 2 = 0

Nós temos a relação

V 1 = Q 1 A 1 ⇒ Q 1 = V 1 A 1

Assim, podemos substituir na equação para termos:

∂ ∂ t M V C - ρ Q 1 + ρ V 2 A 2 = 0

∂ ∂ t M V C = ρ Q 1 - ρ V 2 A 2

∂ ∂ t M V C = ρ Q 1 - V 2 A 2

Passo 3

Gravidade específica pode ser expressa pela relação

S G = ρ ó l e o ρ á g u a

ρ ó l e o = S G × ρ á g u a

Substituindo o valor de ρ na equação encontrada no passo 2 obtemos:

∂ ∂ t M V C = S G × ρ á g u a Q 1 - V 2 A 2

Passo 4

Na literatura, a gravidade específica do óleo hidráulico é S G = 0,88 .

A densidade da água é  ρ á g u a = 1000   k g / m 3 .

A área na saída é A 2 = π 4 D 2 2 .

Agora, podemos substituirmos os valores conhecidos na equação encontrada no passo 3. Assim temos:

∂ ∂ t M V C = S G × ρ á g u a Q 1 - V 2 A 2

∂ ∂ t M V C = S G × ρ á g u a Q 1 - V 2 π 4 D 2 2

∂ ∂ t M V C = 0,88 × 1000 k g m 3 0,00036   m 3 s - 1,3 m s × π 4 0,032   m 2

∂ ∂ t M V C = 880 k g m 3 0,00036   m 3 s - 1,046 × 10 - 3 m 3 s

∂ ∂ t M V C = 880 k g m 3 - 6,86 × 10 - 4 m 3 s

∂ ∂ t M V C = - 0,603 k g s

O valor negativo indica que a massa está diminuindo o volume de controle.

Passo 5

Dissemos no passo 2 que:

∂ ∂ t ∫ C V   ρ d ∀ = ∂ ∂ t M V C

Podemos dizer então que:

M V C = ρ ó l e o ∀ ó l e o

Assim, temos a seguinte relação:

∂ M V C ∂ t = ∂ ∂ t ρ ó l e o ∀ ó l e o

Podemos dizer que o óleo é um liquido incompressível, logo ele não varia no tempo. Assim temos:

∂ M V C ∂ t = ρ ó l e o ∂ ∀ ó l e o ∂ t

∂ ∀ ó l e o ∂ t = 1 ρ ó l e o × ∂ M V C ∂ t

∂ ∀ ó l e o ∂ t = 1 S G × ρ á g u a × ∂ M V C ∂ t

Podemos agora substituir os valores conhecidos para obtermos a taxa à qual o acumulador ganha ou perde óleo hidráulico.

∂ ∀ ó l e o ∂ t = 1 0,88 × 1000 k g m 3 × - 0,603 k g s

∂ ∀ ó l e o ∂ t = - 6,855 × 10 - 4 m 3 s

∂ ∀ ó l e o ∂ t = - 0,69 L s

Portanto, a taxa à qual o acumulador ganha ou perde óleo hidráulico é - 0,69   L / s .

Resposta

∂ ∀ ó l e o ∂ t = - 0,69 L s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A placa da figura tem uma área de 2m 2 e espessura desprezível. Entre a placa e o solo existe um fluido que escoa formando um diagrama de velocidades bidimensional dado por v = 20 y v m á x ( 1 - 5 y
No sistema da figura, A 3 = 0,5m 2 , ρ 3 = 0,4k g / m 3 e os fluidos são gases. No sistema da figura, o óleo fornecido pela bomba mantém o pistão parado. O óleo escoa através da folga entre o pistão e
O tanque da figura abaixo permanece em nível constante. O escoamento na calha tem uma seção transversal quadrada e é bidimensional, obedecendo à equação v = 3 y 2 . Sabendo que o tanque B tem 1m 3 e é
O esquema a seguir corresponde à seção longitudinal de um canal de 25c m de largura. Admitindo escoamento bidimensional e sendo o diagrama de velocidades dado por v = 30 y - y 2 ( ye mc m ; ve mc m /
No sistema da figura, A 3 = 0,5m 2 , ρ 3 = 0,4k g / m 3 e os fluidos são gases. Dados: Seção ( 1 ) : v = 4 1 - r R 2 ; Q 1 = 2m 3 / s ; ρ 1 = 0,6k g / m 3 Seção ( 2 ) : v = 9 1 - r 0,4 ; ρ 2 = 1,2k g