Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 3.Exercício - Ex. 19

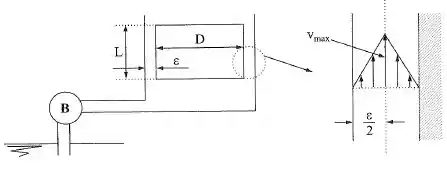
No sistema da figura, A 3 = 0,5   m 2 , ρ 3 = 0,4   k g / m 3 e os fluidos são gases. No sistema da figura, o óleo fornecido pela bomba mantém o pistão parado. O óleo escoa através da folga entre o pistão e o cilindro com uma distribuição linear de velocidades, tendo a máxima velocidade na linha de centro da seção de escoamento. Calcular a vazão de óleo que deve ser fornecida pela bomba adotando a área da coroa circular igual π D ε .

Dados:

Pressão na base do pistão = 50   k P a

L = 2   m ; D = 20   c m ; p e s o   d o   p i s t ã o = 520 π   N

μ = 5 × 10 - 3   N ⋅ s / m 2 ; ε = 1   m m

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Para a resolução da questão, é fornecida a área da coroa, e utilizaremos a seguinte equação:

p ⋅ π D 2 4 + μ v m á x ε 2 ⋅ π ⋅ D ⋅ L = 520 π

v m = v m á x 2

A = π D ε

E:

Q = v m ⋅ A

Passo 2

Encontraremos o valor da velocidade máxima através da primeira equação fornecida portanto, ficaremos com:

p ⋅ D 2 4 + μ v m á x ε 2 ⋅ D ⋅ L = 520

2 μ v m á x ε ⋅ D ⋅ L = 520 - p ⋅ D 2 4

v m á x = ε 520 - p ⋅ D 2 4 2 μ D L

Substituindo os valores, temos que:

v m á x = 10 - 3 520 - 50000 ⋅ 0,2 2 4 2 5 ⋅ 10 - 3 ( 0,2 ) ( 2 )

Resolvendo, temos que:

v m á x = 5   m / s

Passo 3

A velocidade média, é metade da velocidade máxima para o escoamento laminar, portanto:

v m = v m á x 2

v m = 5 2

v m = 2,5   m / s

Passo 4

Com o valor da velocidade média, podemos descobrir a vazão:

Q = v m A

Q = v m π D ε

Substituindo os valores, temos que:

Q = 2,5 ⋅ π ⋅ 0,2 ⋅ 10 - 3

Q = 1,57 ⋅ 10 - 3   m 3 / s

Logo:

Q = 1,57   L / s

Resposta

Q = 1,57   L / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um agricultor de arroz necessita encher de água uma área de plantio de 150 m × 400 m, com uma profundidade de 7,5 cm em 1 h. Quantos tubos de suprimento de água com 37,5 cm de diâmetro são necessários
Considere o escoamento incompressível e permanente através do dispositivo mostrado. Determine o módulo e o sentido da vazão volumétrica através da porta 3.
Um fluido, com massa específica de 1.040 kg/m3, flui em regime permanente através da caixa retangular mostrada. Dados A 1 = 0,046m 2 , A 2 = 0,009m 2 , A 3 =0,056m 2 , V → =3 i ^m / s e V → = 6 j ^m /
A área sombreada mostrada está em um escoamento onde o campo de velocidade é dado por V → = a x i ^ = b y j ^ + c k ^ ; a = b = 2s - 1 e c = 1m / s . Escreva uma expressão vetorial para um elemento da
Um campo de velocidade na região mostrada dado por V → = a j ^ + b y k ^ , em que a=10m / s e b=5s - 1 . Para o volume de controle triangular de 1 m = 1 m (com profundidade w=1m perpendicular ao diagr