Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 10.Exercício - Ex. 5
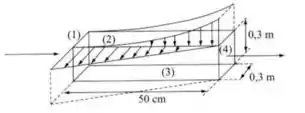
Após a seção de entrada (1) de um conduto de seção quadrada de , existem duas paredes porosas. A vazão de água na entrada é . Pela parede porosa superior (2) há uma vazão de entrada que varia parabolicamente, por unidade de largura, desde na seção (1) até , junto à seção (4). Na outra face porosa (3), a água sai com uma vazão que varia linearmente, por unidade de largura, desde à seção (1), até , junto à seção (4). Determinar a vazão na seção (4) de saída do conduto, localizada a de entrada (1).
Passo 1
Pela equação da continuidade nós temos:
Primeiro, vamos considerar que o fluido é incompressível , então podemos simplificar a densidade:
Vamos fazer a seguinte consideração: O volume de líquido dentro do Volume de Controle é constante, o regime é permanente e o volume , logo a sua derivada é igual a zero:
A expressão restante representa o volume que atravessa a superfície de controle. Este fluxo de fluido é composto pela entrada em e , e pelas saídas em e .
Já possuímos o valor da vazão de entrada em (1)
Os valores de e podem ser determinados pela VOLUME da região abaixo das curvas. Geralmente os erros nessa questão ocorrem por considerarmos apenas as áreas abaixo das curvas.
Passo 2
A distribuição de vazão na seção (2) é:
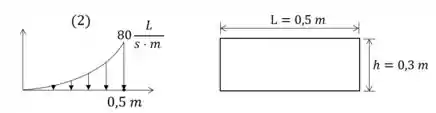
Como é uma distribuição parabólica sabemos que ela se comporta na forma:
Quando :
Se considerarmos que o ponto é um ponto de mínimo da função, então:
Quando
Assim, chegamos numa equação:
A vazão em um ponto da região é dada por:
Efetuando a integração:
Passo 3
Para o fluxo de saída em temos a seguinte distribuição:
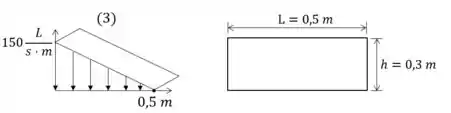
A vazão é dada pela área abaixo da curva. Como o gráfico forma um triângulo podemos calcular pela área do triângulo
Passo 4
A vazão em (4) é: