Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 8º - Capítulo 3.Problemas - Ex. 69
Um aquecedor de ar pode ser fabricado pelo enrolamento de um fio de níquel cromo e passagem do ar em escoamento cruzado ao fio. Considere um aquecedor fabricado com um fio de diâmetro , resistividade elétrica, , condutividade térmica, , e emissividade . O aquecedor é projetado para fornecer ar a uma temperatura de sob condições de escoamento que fornecem um coeficiente convectivo de na superfície do fio. A temperatura do envoltório que envolve o fio e através do qual o ar escoa é igual a .
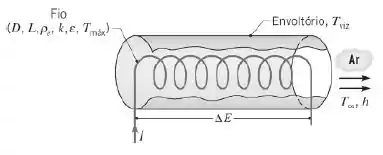
Se a temperatura máxima admissível do fio é igual a , qual é a corrente elétrica máxima admissível, ? Se a voltagem máxima disponível é de , quais são o comprimento do fio que pode ser usado no aquecedor e a potência nominal do aquecedor? Sugestão: Na sua solução, suponha variação de temperatura no interior do fio desprezível, mas após obter os resultados desejados, avalie a validade desta suposição.
Passo 1
Fala Galera!! Bora resolver essa questão comigo??
Nessa questão queremos determinar a corrente elétrica operacional máxima admissível, o comprimento do fino no aquecedor e potência nominal do aquecedor.
PRESSUPOSTOS:
(1) Estado estacionário;
(2) Temperatura uniforme do fio;
(3) Propriedades constantes;
(4) Troca de radiação em ambientes grandes.
DADOS FORNECIDOS:
Diâmetro do fio de níquel cromo do aquecedor:
Raio do fio de níquel cromo do aquecedor:
Resistividade elétrica:
Emissividade:
Condutividade térmica do fio de níquel cromo:
Coeficiente convectivo entre o ar e o fio:
Temperatura do ar fornecida pelo aquecedor:
Temperatura do envoltório que envolve o fio através do qual o ar escoa:
Temperatura máxima admissível do fio:
Voltagem máxima disponível:
Passo 2
Para resolver essa questão, vamos assumir uma temperatura uniforme do fio, assim,
Temos também que a geração volumétrica máxima de calor pode ser obtida pela equação 3.60
onde é o coeficiente total de transferência de calor, , usado no lugar do coeficiente de convecção da formula acima.
Passo 3
Agora, vamos calcular a o coeficiente de transferência de calor por radiação usando a seguinte relação:
Aqui, é emissividade, é a constante Boltzmann de Stefan, é a temperatura da superfície e é a temperatura do envoltório que envolve o fio. Substituindo os termos da equação acima pelos dados fornecidos, temos:
Assim, temos que o coeficiente total de transferência de calor é o seguinte:
Passo 4
Com o coeficiente total de transferência de calor, podemos obter a taxa máxima de geração de energia por unidade de volume usando a expressão citada no passo 2. Assim temos:
Substituindo os termos da equação acima pelos dados fornecidos, temos:
Passo 5
Podemos calcular a corrente elétrica operacional máxima permitida, usando a equação 3.43, em que:
Aqui, é a resistência elétrica, é a corrente elétrica e é o volume do fio.
Reorganizando, temos:
Aqui, é a resistividade elétrica e é o raio do fio. Substituindo os termos da equação acima pelos dados fornecidos, temos:
Portanto, a corrente operacional máxima permitida é .
Passo 6
Podemos calcular o comprimento do fio do aquecedor correspondente à corrente de operação utilizando a seguinte relação:
Reorganizando:
Aqui, é a tensão máxima disponível, é a área da seção transversal, é a corrente elétrica máxima permitida, é a resistividade elétrica e é o raio do fio do aquecedor. Substituindo os termos da equação acima pelos dados fornecidos, temos:
Portanto, o comprimento do fio do aquecedor é .
Passo 7
Agora, vamos calcular a potência nominal do aquecedor usando a seguinte relação:
Aqui é a mudança no potencial elétrico e é a corrente operacional máxima permitida. Substituindo os termos da equação acima pelos dados fornecidos, temos:
Portanto, a potência nominal do aquecedor é .