Enunciado
Cálculo Numérico - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 4.Problemas - Ex. 79
Uma barra com de diâmetro e de comprimento tem uma de suas extremidades mantida a Na superfície da barra há transferência de calor por convecção natural com o ar ambiente a e um coeficiente convectivo que depende da diferença entre as temperaturas da superfície e do ar ambiente. Especificamente, o coeficiente é estabelecido por uma correlação que tem a forma , na qual as unidades são e A superfície da barra tem uma emissividade e troca calor por radiação com a vizinhança a . Na extremidade da aleta também há convecção natural e troca de calor por radiação.
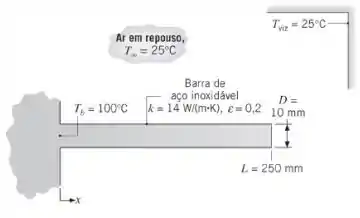
Supondo condução unidimensional e usando um método de diferenças finitas, representando a aleta por cinco nós, estime a distribuição de temperaturas na aleta. Determine também a taxa de transferência de calor na aleta e as contribuições relativas da convecção natural e da radiação. Sugestão: Para cada nó que necessite de um balanço de energia, use a forma linearizada da equação para a taxa radiante, Equação 1.8, com o coeficiente de transferência de calor por radiação , Equação 1.9, calculado para cada nó. Da mesma forma, na equação para a taxa de transferência de calor por convecção natural associada a cada nó, o coeficiente convectivo deve ser calculado em cada nó.
Passo 1
Nessa questão nós temos uma aleta de pino de de diâmetro e comprimento com temperatura base de experimentando troca de radiação com o ambiente e convecção livre com o ar ambiente.
Com isso, queremos encontrar a distribuição de temperatura pelo método das diferenças finitas com cinco nós, a taxa de calor da aleta e contribuições relativas por convecção e radiação. Então vamos lá!
Passo 2
Para resolver essa questão vamos assumir:
(1) Condições em estado estacionário;
(2) Condução unidimensional na aleta;
(3) Propriedades constantes;
(4) A aleta é um objeto pequeno em um recinto grande;
(5) A ponta da aleta experimenta convecção e radiação;
(6) .
Para aplicar o método da diferença finita, temos que . E podemos fazer os balanços de energia nos nós para obter as equações de diferença finita para as temperaturas nodais.
Nó interior,
Onde o coeficiente de convecção livre é:
E o coeficiente de radiação linearizado é,
Com,
e
Passo 3
Para o nó da ponta,
Conhecendo as temperaturas nodais, as taxas de calor são avaliadas como:
Taxa de aquecimento da aleta: um balanço de energia em torno do nó b.
Onde e são avaliados em .
Passo 4
Passo 4 Taxa de calor por convecção: Para determinar a parte da taxa de calor por convecção a partir da superfície da aleta, precisamos somar as contribuições de cada nó. Utilizando os termos da taxa de calor de convecção dos balanços de energia anteriores, respectivamente para o nó , os nós e o nó ,
Taxa de calor de radiação: da mesma maneira,
As equações acima foram inseridas no espaço de trabalho IHT e o conjunto de equações resolvido para as temperaturas nodais e as taxas de calor. Os principais resultados, incluindo a distribuição de temperatura e as taxas de calor, é mostrado abaixo.
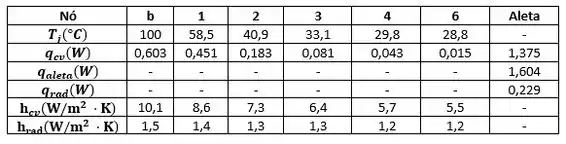
Resposta
