Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo Numérico - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 4.Problemas - Ex. 48

Seja a malha bidimensional ( ∆ x = ∆ y ) representando condições de regime estacionário, sem geração volumétrica interna de calor, em um sistema com condutividade térmica k . Um dos contornos é mantido a uma temperatura constante T s , enquanto os demais são adiabáticos.

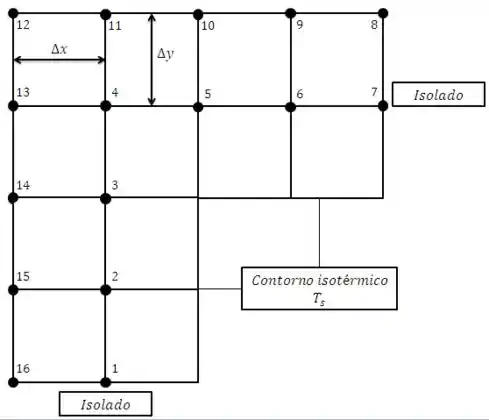
Desenvolva uma expressão para a taxa de transferência de calor cruzando o contorno isotérmico ( T s ) , por unidade de comprimento normal à página.

Passo 1

Nosso primeiro passo será desenhar o volume de controle para esse sistema e identificar as taxas de transferência de calor que atravessam o sistema:

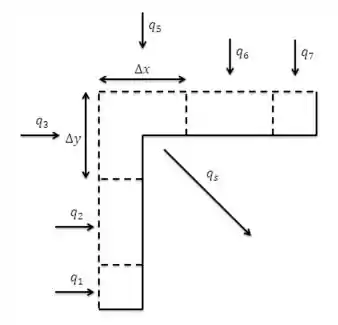
O balanço de energia para este volume de controle em regime estacionário é:

E ˙ e n t - E ˙ s a í d a + E ˙ g e r = 0

E ˙ e n t - E ˙ s a í d a = 0

q 1 + q 2 + q 3 + q 5 + q 6 + q 7 - q s = 0

Passo 2

Vamos descrever cada uma das taxas de transferência separadamente:

q 1 = k A 1 L 1 ∆ T 1

q 1 = k ∆ y 2 ∙ 1 ∆ x ( T 1 - T s )

q 2 = k A 2 L 2 ∆ T 2

q 2 = k ∆ y ∙ 1 ∆ x ( T 2 - T s )

q 3 = k A 3 L 3 ∆ T 3

q 3 = k ∆ y ∙ 1 ∆ x ( T 3 - T s )

q 5 = k A 5 L 5 ∆ T 5

q 5 = k ∆ x ∙ 1 ∆ y ( T 5 - T s )

q 6 = k A 6 L 6 ∆ T 6

q 6 = k ∆ x ∙ 1 ∆ y ( T 6 - T s )

q 7 = k A 7 L 7 ∆ T 7

q 7 = k ∆ x 2 ∙ 1 ∆ y ( T 7 - T s )

Passo 3

Substituindo no balanço de energia:

q s = k ∆ y 2 ∙ 1 ∆ x T 1 - T s + k ∆ y ∙ 1 ∆ x T 2 - T s + k ∆ y ∙ 1 ∆ x T 3 - T s + k ∆ x ∙ 1 ∆ y T 5 - T s + k ∆ x ∙ 1 ∆ y T 6 - T s + k ∆ x 2 ∙ 1 ∆ y ( T 7 - T s )

Considerando ∆ x = ∆ y :

q s = k 2 T 1 - T s + k T 2 - T s + k T 3 - T s + k T 5 - T s + k T 6 - T s + k 2 ( T 7 - T s )

q s = k 0,5 T 1 + T 2 + T 3 + T 5 + T 6 + 0,5 T 7 - 5 T s

Resposta

A taxa de calor que atravessa o contorno isotérmico é:

q s = k 0,5 T 1 + T 2 + T 3 + T 5 + T 6 + 0,5 T 7 - 5 T s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A condução no interior de geometrias relativamente complexas pode, às vezes, ser avaliada usando métodos de diferenças finitas deste livro, que podem ser aplicados em subdomínios e depois unidos. Cons
As temperaturas (°C), em regime estacionário, associadas a pontos nodais selecionados em um sistema bidimensional com uma condutividade térmica de 1,5 W m K , são mostradas na malha mostrada na figura
Seja uma longa barra com seção transversal quadrada (0,8 m de lado) e condutividade térmica de 2 W m K . Três laterais da barra são mantidas a uma temperatura uniforme de 300°C. A quarta superfície es
Uma análise por diferenças finitas, em condições de regime estacionário, foi efetuada em uma aleta cilíndrica com um diâmetro de 12 mm e condutividade térmica de 15 W m K . O processo de transferência
Considere uma aleta plana triangular, bidimensional, com comprimento L = 50 mm e espessura na base de t = 20 mm. A condutividade térmica da aleta é k=25 W m K . A temperatura de sua base é T b=50 ° C