As superfícies superior e inferior de uma barra de condução são resfriadas por convecção com ar a T ∞ , com h s ≠ h i . As laterais são resfriadas pela manutenção de contato com sumidouro de calor a T 0 , através de uma resistência térmica de contato R t , c ' ' . A barra tem uma condutividade térmica k e a sua largura é igual a duas vezes a sua espessura L .Considere condições de regime estacionário, nas quais o calor é gerado uniformemente a uma taxa volumétrica q ˙ devido à passagem de uma corrente elétrica. Usando o método do balanço de energia, deduza as equações de diferenças finitas para os pontos nodais de 1 e 13 .

Ponto 1 : T 2 + T 6 + ∆ x k R t , c ' ' T 0 + h s ∆ x k T ∞ - 2 ∆ x 2 k R t , c ' ' + h s ∆ x k + 1 T 1 = - q ˙ ∆ x 2 2 k Ponto 13 : T 12 + T 14 + 2 T 8 + 2 h i ∆ x k T ∞ - 2 2 + h i ∆ x k T 13 = - q ˙ ∆ x 2 k

Enunciado

Cálculo Numérico - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 4.Problemas - Ex. 45

As superfícies superior e inferior de uma barra de condução são resfriadas por convecção com ar a , com . As laterais são resfriadas pela manutenção de contato com sumidouro de calor a , através de uma resistência térmica de contato . A barra tem uma condutividade térmica e a sua largura é igual a duas vezes a sua espessura .

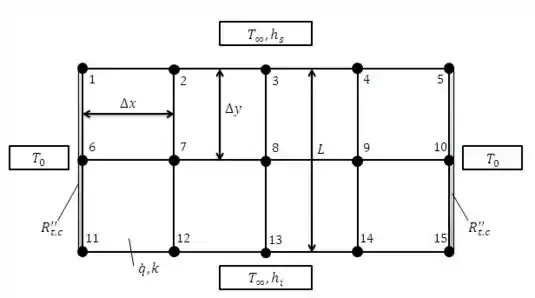
Considere condições de regime estacionário, nas quais o calor é gerado uniformemente a uma taxa volumétrica devido à passagem de uma corrente elétrica. Usando o método do balanço de energia, deduza as equações de diferenças finitas para os pontos nodais de e .

Passo 1

O exercício nos dá um sistema em que devemos obter a equação de diferenças finitas para dois pontos. Vamos começar pelo ponto . O primeiro passo é desenhar o volume de controle para este ponto:

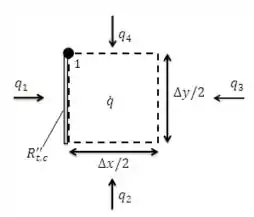
O balanço de energia em regime estacionário é:

Passo 2

Vamos agora escrever cada uma das taxas separadamente:

Substituindo no balanço de energia:

Considerando :

Passo 3

Vamos agora definir a equação de diferenças finitas para o ponto 13. O primeiro passo é definir o volume de controle e as taxas de transferência de calor que chegam ao sistema:

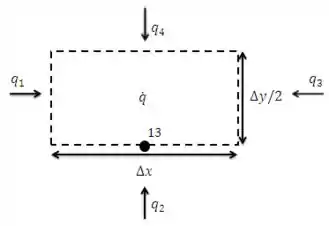
O balanço de energia para esse ponto nodal é:

Temos agora que obter as expressões para cada taxa de transferência de calor:

Substituindo no balanço de energia:

Considerando :

Resposta

Ponto :

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

As temperaturas (em K), em regime estacionário, de três pontos nodais de uma longa barra retangular são fornecidas na figura. A barra experimenta uma taxa de geração volumétrica de calor uniforme igua

Seja o canal quadrado mostrado na figura, operando sob condições de regime estacionário. A superfície interna do canal está a uma temperatura uniforme de 600 K, enquanto a superfície externa está expo

Seja o tubo bidimensional de seção transversal não circular formado por subdomínios retangular e semicilíndrico unidos pelas superfícies de controle comuns, representadas pela linha tracejada, de form

Temperaturas em regime estacionário em pontos nodais escolhidos da seção simétrica de um canal de escoamento são conhecidas: T 2 = 95,47 ° C , T 3 = 117,3 ° C , T 5 =79,79 ° C , T 6 =77,29 ° C , T 8 =

Seja um dissipador de calor de alumínio k=240 W m K , como o mostrado esquematicamente no Problema 4.28. As larguras interna e externa do canal quadrado são w = 20 mm e W = 40 mm, respectivamente, e u