Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo Numérico - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 4.Problemas - Ex. 41

Um dos pontos fortes dos métodos numéricos é a sua capacidade de lidar com condições de contorno complexas. No esboço, a condição de contorno muda de fluxo térmico especificado, q s ' ' (para dentro do domínio), para convecção, na posição do nó (m,n). Escreva a equação de diferenças finitas bidimensional, em regime estacionário, neste nó.

Passo 1

Vamos começar desenhando as taxas de transferência de calor no volume de controle:

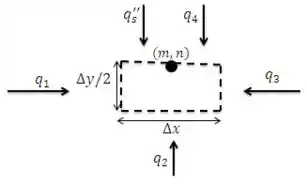
Vamos agora aplicar o balanço de energia a esse volume de controle em regime estacionário:

d E d t = E ˙ e n t - E ˙ s a í d a

0 = E ˙ e n t

0 = q 1 + q 2 + q 3 + q 4 + q s ' ' A s

Passo 2

Vamos agora calcular separadamente cada taxa de transferência de calor:

q 1 = q ( m - 1 , n ) → ( m , n )

q 1 = k A ∆ T L

q 1 = k ∆ y 2 ∙ 1 ∆ x T m - 1 , n - T m , n

q 2 = q ( m , n - 1 ) → ( m , n )

q 2 = k A L ∆ T

q 2 = k ∆ x ∙ 1 ∆ y T m , n - 1 - T m , n

q 3 = q ( m + 1 , n ) → ( m , n )

q 3 = k A L ∆ T

q 3 = k ∆ y 2 ∙ 1 ∆ x T m + 1 , n - T m , n

q 4 = q c o n v , y

q 4 = h A ∆ T

q 4 = h ∆ x 2 ∙ 1 T ∞ - T m , n

q 5 = q s ' ' A s

q 5 = q s ' ' ∆ x 2 ∙ 1

Passo 3

Substituindo no balanço de energia:

k ∆ y 2 ∙ 1 ∆ x T m - 1 , n - T m , n + k ∆ x ∙ 1 ∆ y T m , n - 1 - T m , n + k ∆ y 2 ∙ 1 ∆ x T m + 1 , n - T m , n + h ∆ x 2 ∙ 1 T ∞ - T m , n + q s ' ' ∆ x 2 ∙ 1 = 0

Para ∆ x = ∆ y :

k 2 T m - 1 , n - T m , n + k T m , n - 1 - T m , n + k 2 T m + 1 , n - T m , n + h ∆ x 2 T ∞ - T m , n + q s ' ' ∆ x 2 = 0

T m - 1 , n - T m , n + 2 T m , n - 1 - T m , n + T m + 1 , n - T m , n + h ∆ x k T ∞ - T m , n + q s ' ' ∆ x k = 0

T m - 1 , n + 2 T m , n - 1 + T m + 1 , n + h ∆ x k T ∞ - 4 + h ∆ x k T m , n = - q s ' ' ∆ x k

Resposta

T m - 1 , n + 2 T m , n - 1 + T m + 1 , n + h ∆ x k T ∞ - 4 + h ∆ x k T m , n = - q s ' ' ∆ x k

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Seja a configuração nodal 2 da tabela 4.2 . Deduza as equações de diferenças finitas, para condições de regime estacionário, nas seguintes situações.(a) O contorno horizontal do vértice interno está p
Em uma configuração cilíndrica bidimensional, os espaçamentos radiais ( ∆ r ) e angulares ( ∆ φ ) entre os pontos nodais são uniformes. O contorno em r = r , está em uma temperatura uniforme T i . Na
Materiais funcionalmente graduados são intencionalmente fabricados para estabelecerem uma distribuição espacial de propriedades no produto final. Seja um objeto L × L bidimensional, com L = 20 mm. A d
Um canal por onde passam gases quentes de exaustão apresenta uma seção transversal quadrada de 300 mm de lado. As paredes são construídas com tijolos refratários com 150 mm de espessura e condutividad
Uma longa barra condutora com seção transversal retangular ( 20m m×30m m ) e condutividade térmica k=20 W m K , experimenta geração térmica uniforme a uma taxa de q ˙ =5×10 7 W m 3 , enquanto suas sup