Seja o elemento combustível do Exemplo . Inicialmente, o elemento está a uma temperatura uniforme de sem geração de energia. Subitamente, o elemento é inserido no núcleo do reator passando a ter uma taxa volumétrica de geração de energia uniforme . As superfícies são resfriadas por convecção com e . Usando o método explícito com um incremento espacial de , determine a distribuição de temperaturas após o elemento ser inserido no núcleo do reator.
Passo 1
Vamos lá! Nosso problema pede a distribuição de temperatura pra um incremento de , mas antes vamos fazer um esboço para facilitar nossa vida.
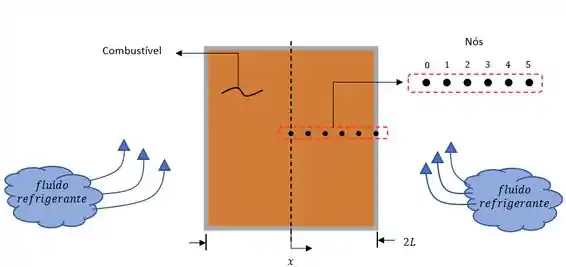
Agora precisamos fazer nossas famosas considerações. Hehe (u.u)
Passo 2
Vamos lá, com nossos dados em mãos vamos calcular a distribuição de temperatura pelo método explicito, como foi sugerido pelo problema, assim iremos usar as mesmas equações de diferença finita para nossa rede nodal do exemplo . Então temos:
Nos nós interiores, .
No nó central, .
E no nó de superfície, .
Passo 3
Agora temos que o critério de estabilidade mais rígido se encontra nos nós de superfície em ambos os lados, pois não pode ser menor que , assim:
Organizando
Calculando o número de temos:
Assim:
Como , vamos encontrar agora os intervalos de tempo, assim temos:
Para não trabalharmos com números muito quebrados e ficarmos bem com nosso critério de estabilidade, vamos arredondar , Assim:
Por fim o tempo será dado por:
Passo 4
Agora vamos substituir todos os dados que encontramos nas nossas equações dos nós, com , assim temos:
Fazendo o mesmo processo para as demais temos:
Passo 5
Agora vamos fazer uma tabela com nossos dados para intervalos, como a temperatura inicial é temos:
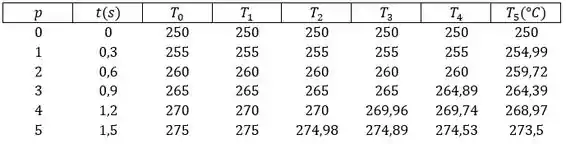
P.S: vale ressaltar que nos instantes iniciais do processo, o plano central não vai sentir o efeito do ar refrigerante.
Isso é tudo pessoal! \o/

Resposta
Ei, a resposta está no passo a passo :)