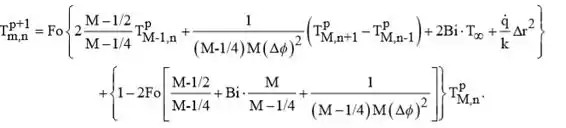Enunciado
Cálculo Numérico - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 5.Problemas - Ex. 138
Um cabo elétrico, que experimenta uma geração volumétrica de calor a uma taxa uniforme , encontra-se semienterrado em um material isolante, enquanto a sua superfície superior está exposta a um processo convectivo (T∞, h).
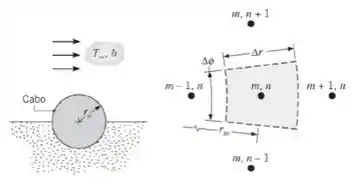
(a)Deduza as equações de diferenças finitas, pelo método explícito, para um nó interior (); para o nó central (); e para os nós na superfície externa () no contorno isolado termicamente e no contorno sujeito ao processo convectivo.
(b)Obtenha o critério de estabilidade para cada uma das equações de diferenças finitas. Identifique o critério mais restritivo.
Passo 1
Vamos lá gente!! As equações explícitas e de diferença finita podem ser obtidas aplicando balanços energéticos a volumes de controle apropriados sobre o nó de interesse. Observe o sistema de coordenadas definido acima onde . O critério de estabilidade é determinado a partir do coeficiente associado ao nó de interesse. A conservação de energia necessária é:
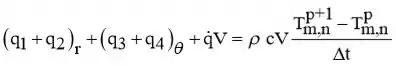
Destrinchando cada valor implícito, temos:
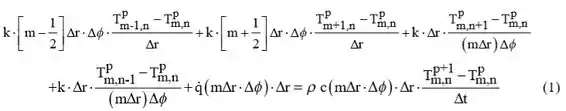
Passo 2
Vamos definir o número de Fourier como:
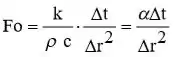
E então reagrupamos os termos da equação 1 para obter FDE,
Passo 3
O critério de estabilidade exige que o último termo do lado direito em aparelho seja positivo. Ou seja, o coeficiente de deve ser positivo e o critério de estabilidade é
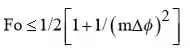
Por inspeção, o critério de estabilidade é . Nós de Superfície (). O volume de controle para o nó de superfície é . A partir do balanço energético,
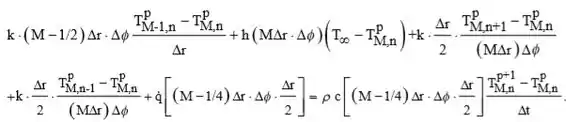
Reagrupamento e utilização das definições para e ,
