Enunciado
Cálculo Numérico - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 4.Problemas - Ex. 64
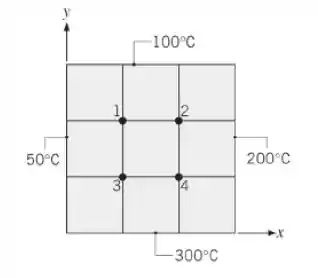
Seja a condução bidimensional, em regime estacionário, em uma seção transversal quadrada com temperaturas superficiais especificadas.
- Determine as temperaturas nos nós 1, 2, 3 e 4. Estime a temperatura no ponto central.
- Reduzindo à metade o tamanho da malha, determine as temperaturas nodais correspondentes. Compare os seus resultados com os obtidos com a malha mais grossa.
- Com os resultados para a malha mais fina, represente as isotermas a 75, 150 e 250°C.
Passo 1
Boom galerinha, vamos começar?
Preparar, apontar e jaaa !!
Para todos os pontos nós temos um nó no interior, quando é assim nós podemos usar a fórmula:
Para o Ponto 1:
Para o Ponto 2:
Para o Ponto 3:
Para o Ponto 4:
Resolvendo as quatro equações simultaneamente usando um software ou usando o método de iteração de Gauss Seidel, obtemos:
Então a única coisa que nós precisamos fazer é achar o ponto central, ok?
E para isso é só fazer a média:
Passo 2
Na letra (b) nós queremos reduzir à metade o tamanho da malha e determinar as temperaturas nodais correspondentes, ok?
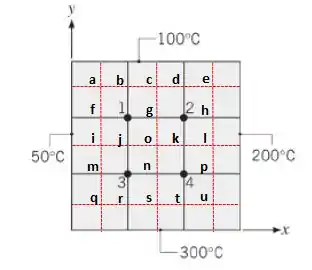
Como todos são pontos internos nós faremos a mesma coisa que fizemos no Passo 1, ok?
Usaremos as mesmas equações e acharemos os pontos “intermediários”:
Quando resolvemos as equações simultaneamente:
Então a única coisa que nós precisamos fazer é achar o ponto central, ok?
E para isso é só fazer a média:
Passo 3
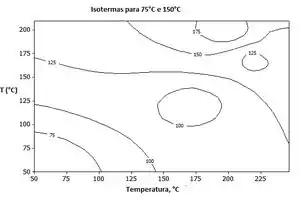
Na letra (c) nós queremos representar isotermas, para isso nós vamos lançar as equações do Passo 2 no menu do software IHT e vamos obter os seguintes dados:
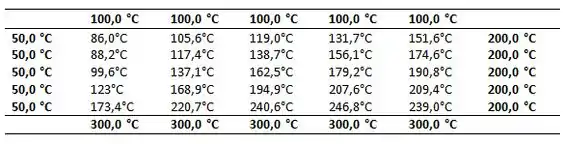
E plotando:
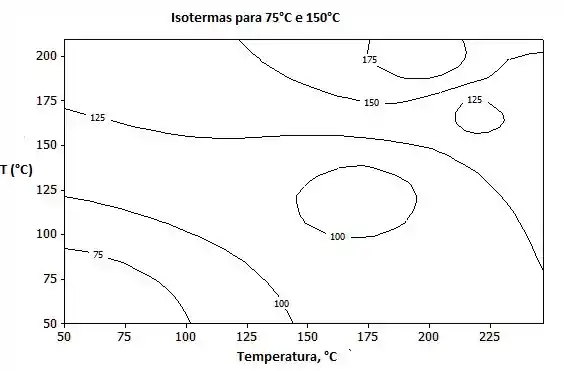
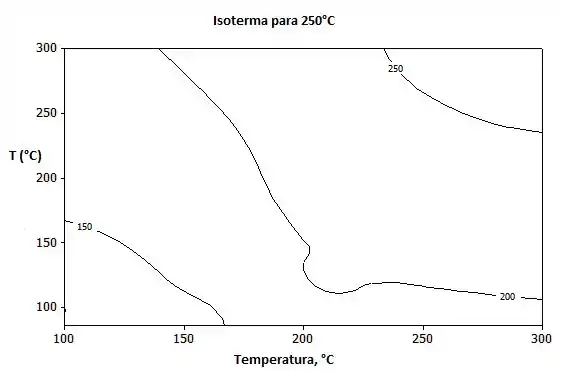
E acabamos mais uma galerinhaa !!
