Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo Numérico - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 4.Problemas - Ex. 65

Seja uma longa barra com seção transversal quadrada (0,8 m de lado) e condutividade térmica de 2 W m K . Três laterais da barra são mantidas a uma temperatura uniforme de 300°C. A quarta superfície está exposta a um fluido a 100°C, com um coeficiente de transferência de calor por convecção igual a 10 W m 2 K .

  1. Usando uma técnica numérica apropriada com um espaçamento na malha de 0,2 m, determine a temperatura no ponto central e a taxa de transferência de calor, por unidade de comprimento da barra, entre a barra e o fluido.
  2. Reduzindo à metade o espaçamento na malha, determine a temperatura no ponto central e a taxa de transferência de calor. Represente graficamente a distribuição de temperaturas correspondente ao longo da superfície exposta ao fluido. Represente também as isotermas a 200 e 250°C.

Passo 1

Boom galerinha, vamos começar?

Desenhando o que está acontecendo aqui:

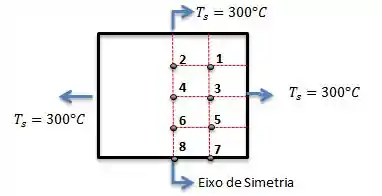
Para todos os pontos 1, 2, 3, 4, 5 e 6, nós temos um nó no interior, quando é assim nós podemos usar a fórmula:

T i = 1 4 ∑ T v i z i n h o s

Para o Ponto 1:

4 T 1 = T 2 + T 3 + 600

Para o Ponto 2:

4 T 2 = 2 T 1 + T 4 + 3 00

Para o Ponto 3:

4 T 3 = T 1 + T 4 + T 5 + 3 00

Para o Ponto 4:

4 T 4 = T 2 + 2 T 3 + T 6

Para o Ponto 5:

4 T 5 = T 3 + T 6 + T 7 + 300

Para o Ponto 6:

4 T 6 = T 4 + 2 T 5 + T 8

Os pontos 7 e 8 estão em uma superfície om convecção, certo?

Para o Ponto 7:

4 T 7 = 2 T 5 + T 8 + 500

Para o Ponto 8:

4 T 8 = 2 T 7 + 2 T 6 + 200

Quando resolvemos as equações simultâneas:

T 1 = 292,2 ° C

T 2 = 289,2 ° C

T 3 = 279,7 ° C

T 4 = 272,2 ° C

T 5 = 254,2 ° C

T 6 = 240,1 ° C

T 7 = 198,1 ° C

T 8 = 179,4 ° C

Mas nós queremos a temperatura no ponto central e a taxa de transferência de calor, por unidade de comprimento da barra, entre a barra e o fluido, certo?

O ponto central é o Ponto 4, então:

T c e n t r a l = 272,2 ° C

O calor por convecção ocorre entre os pontos 7, 8 e a superfície, de ambos os lados, ok?

q ' c o n v = 2 ( q ' 7 + q ' 8 + q ' T s )

Substituindo:

q ' c o n v = 2 h ∆ x 2 T 7 - T ∞ + ∆ x T 8 - T ∞ + ∆ x 2 T ∞ - T s

Colocando nossos dados:

q ' c o n v = 2 10 W m 2 K 0,2   m 2 198,1 ° C - 100 ° C + 0,2   m 179,4 ° C - 100 ° C + 0,2   m 2 300 ° C - 100 ° C

q ' c o n v = 952 W m

Passo 2

Na letra (b) nós queremos reduzir à metade o tamanho da malha e determinar as temperaturas correspondentes, ok?

Como todos são pontos internos, exceto 29, 30, 31 e 32, nós faremos a mesma coisa que fizemos no Passo 1, ok?

Usaremos as mesmas equações e acharemos os pontos “intermediários”:

4 T 1 = 2 T 2 + T 5 + 300

4 T 2 = T 1 + T 6 + T 3 + 300

4 T 3 = T 2 + T 7 + T 4 + 300

4 T 4 = T 3 + T 8 + 6 00

4 T 5 = 2 T 6 + T 1 + T 9

4 T 6 = T 2 + T 5 + T 10 + T 7

4 T 7 = T 3 + T 6 + T 1 1 + T 8

4 T 8 = T 4 + T 7 + T 12 + 300

4 T 9 = 2 T 10 + T 5 + T 13

4 T 10 = T 6 + T 9 + T 1 4 + T 11

4 T 1 1 = T 7 + T 10 + T 1 5 + T 1 2

4 T 1 2 = T 8 + T 1 1 + T 1 6 + 300

4 T 13 = 2 T 1 4 + T 9 + T 1 7

4 T 1 4 = T 10 + T 13 + T 1 8 + T 1 5

4 T 1 5 = T 1 1 + T 1 4 + T 1 9 + T 1 6

4 T 1 6 = T 1 2 + T 1 5 + T 20 + 300

4 T 1 7 = 2 T 1 8 + T 13 + T 21

4 T 1 8 = T 1 4 + T 1 7 + T 22 + T 1 9

4 T 1 9 = T 1 5 + T 1 6 + T 2 3 + T 20

4 T 20 = T 1 6 + T 1 9 + T 2 4 + 300

4 T 21 = 2 T 22 + T 17 + T 25

4 T 22 = T 1 8 + T 21 + T 2 6 + T 23

4 T 2 3 = T 1 9 + T 2 2 + T 2 7 + T 2 4

4 T 2 4 = T 20 + T 23 + T 2 8 + 300

4 T 2 5 = 2 T 2 6 + T 2 1 + T 2 9

4 T 2 6 = T 22 + T 2 5 + T 30 + T 2 7

4 T 2 7 = T 2 3 + T 2 6 + T 3 1 + T 2 8

4 T 2 8 = T 2 4 + T 2 7 + T 3 2 + 300

Os demais estão na superfície que sofre convecção:

5 T 2 9 = 2 T 25 + 2 T 30 + 100

5 T 30 = 2 T 2 6 + T 29 + T 30 + 100

5 T 31 = 2 T 2 7 + T 30 + T 3 1 + 100

5 T 3 2 = 2 T 2 8 + T 3 1 + T 31 + 4 00

Quando resolvemos as equações simultaneamente nós vamos obter temperatura do ponto central, que é o Ponto 13, então:

T c e n t r a l = 271   ° C

E colocando as temperaturas na fórmula da convecção nós obtemos:

q ' c o n v = 834 W m

E acabamos mais uma galerinhaa !!

Resposta

  1. T c e n t r a l = 272,2 ° C       |     q ' c o n v = 952 W m ;
  2. T c e n t r a l = 271 , 0   ° C     |     q ' c o n v = 834 W m .
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a distribuição de temperaturas em t=30m i n para as condições do Problema 5.116 .(a) Use uma técnica de diferenças finitas explícita, com um incremento de tempo de 600s e um incremento no es
Seja o elemento combustível do Exemplo 5.11 . Inicialmente, o elemento está a uma temperatura uniforme de 250 ° C sem geração de energia. Subitamente, o elemento é inserido no núcleo do reator passand
Considere duas placas, A e B, que estão, cada uma, inicialmente isotérmicas e têm espessura L=5m m . As faces das placas são subitamente colocadas em contato em um processo de união. O material A é ac
Considere a folha metálica delgada que atua como malha de aceleração ( k=40W / ( m·K ) ,α=3×10 - 5m 2 / s , ε=0,45 ) , descrita no Problema 4.72. Desenvolva um modelo implícito de diferenças finitas p
Um disco circular delgado está sujeito ao aquecimento por indução a partir de uma bobina, cujo efeito é o de propiciar uma geração uniforme de calor no interior de uma seção anular, conforme mostrado