Para cada um dos casos a seguir, determine um comprimento característico apropriado e o número de Biot correspondente que está associado à resposta térmica transiente do objeto sólido. Diga se a aproximação pela capacitância global é válida. Se a informação da temperatura não for fornecida, avalie as propriedades a .

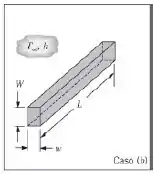
(b) Uma longa barra aquecida de aço inoxidável , com seção transversal retangular, e dimensões , e . A barra está submetida a um refrigerante que fornece um coeficiente de transferência de calor em todas as superfícies expostas.

Agora, vamos substituir os termos para encontrar o comprimento característico. Para uma longa barra de aço inoxidável, temos que a o volume é dado pela expressão

e a área da superfície é dada ela expressão

Aqui,  é a altura da barra de aço,  é a largura da barra de aço e  é o comprimento da barra de aço.

Substituindo as relações encontradas na equação do comprimento característico, temos o seguinte:

Substituindo os termos da equação pelos dados fornecidos, temos:

Portanto, o comprimento característico apropriado que está associado à resposta térmica transitória desse objeto sólido é .

Agora, vamos calcular o número Biot correspondente ao comprimento característico de . Temos que Biot é calculado pela seguinte expressão:

Aqui,   é o coeficiente convectivo,  é o comprimento característico e  é a condutividade térmica do corpo. Substituindo os temos da equação acima pelos dados fornecidos, temos:

Portanto, o número Biot correspondente que está associado à resposta térmica transitória do objeto sólido é . Para que a aproximação da capacitância acumulada seja válida, a condição é

Temos que o número de Biot correspondente ao comprimento característico é menor que , portanto, a aproximação da capacitância global é válida neste caso.