Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 5.Problemas - Ex. 5c
Para cada um dos casos a seguir, determine um comprimento característico apropriado e o número de Biot correspondente que está associado à resposta térmica transiente do objeto sólido. Diga se a aproximação pela capacitância global é válida. Se a informação da temperatura não for fornecida, avalie as propriedades a .
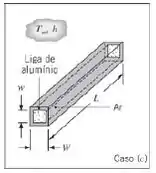
(c) Um longo tudo extrusado de alumínio com dimensões interna e externa e , respectivamente, subitamente submerso em água, com um coeficiente convectivo de nas quatro superfícies externas do tubo. O tubo encontra-se fechado em suas extremidades, o que mantém ar estagnado em seu interior.
Passo 1
(c) Fala galera!!
Dados fornecidos:
Dimensão interna:
Dimensão externa:
Coeficiente convectivo:
Para o alumínio
Condutividade térmica:
Para resolver essa questão, é importante saber que o comprimento característico é a razão da área pelo volume, ou seja:
Aqui, é a área da superfície e é o volume.
Passo 2
Agora, vamos substituir os termos para encontrar o comprimento característico. Para um longo tudo extrusado de alumínio, temos que a o volume é dado pela expressão
Haverá muito pouca transferência de calor para o ar estagnado dentro do tubo, portanto, na determinação da área de superfície para transferência de calor por convecção, somente a área de superfície externa deve ser incluída. Portanto, temos que a área da superfície é dada ela expressão
Aqui, é a dimensão externa, é a dimensão interna e é o comprimento do tubo.
Passo 3
Substituindo as relações encontradas na equação do comprimento característico, temos o seguinte:
Substituindo os termos da equação pelos dados fornecidos, temos:
Portanto, o comprimento característico apropriado que está associado à resposta térmica transitória desse objeto sólido é .
Passo 4
Agora, vamos calcular o número Biot correspondente ao comprimento característico de . Temos que Biot é calculado pela seguinte expressão:
Aqui, é o coeficiente convectivo, é o comprimento característico e é a condutividade térmica do corpo. Substituindo os temos da equação acima pelos dados fornecidos, temos:
Portanto, o número Biot correspondente que está associado à resposta térmica transitória do objeto sólido é . Para que a aproximação da capacitância acumulada seja válida, a condição é
Temos que o número de Biot correspondente ao comprimento característico é menor que , portanto, a aproximação da capacitância global é válida neste caso.