Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 8º - Capítulo 4.Problemas - Ex. 24

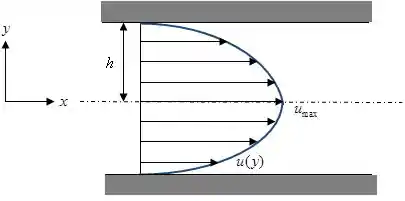
For laminar flow between parallel plates (see Fig. 4.12b),

the flow is two-dimensional (υ ? 0) if the walls are

porous. A special case solution is u 5 (A 2 Bx)(h2 2 y2),

where A and B are constants. (a) Find a general formula for

velocity υ if υ 5 0 at y 5 0. (b) What is the value of the

constant B if υ 5 υ

w at y 5 1h?

Passo 1

Saaaalve, tranquilo? Vamos lá resolver mais uma questão juntos?! 😊

O diagrama mostra o fluxo laminar incompressível bidimensional entre placas paralelas onde as paredes são de meio poroso.

Passo 2

a) Aplicando equação de continuidade em forma bidimensional,

  ∂ u ∂ x + ∂ v ∂ y = 0     ∂ v ∂ y = - ∂ u ∂ x . . . ( 1 )  

Temos a equação

u = ( A - B x ) h 2 - y 2

Substituto ( A - B x ) h 2 - y 2 para u na equação (1)

∂ v ∂ y     = - ∂ ∂ x ( A - B x ) h 2 - y 2   ∂ v ∂ y     = B h 2 - y 2   d v     = B h 2 - y 2 d y  

Passo 3

Integrando a equação acima em ambos os lados,

    ∫   d v = ∫   B h 2 - y 2 d y     v = B h 2 y - y 3 3 + K ( x ) … … ( 2 )  

Aqui, é K ( x ) a constante de integração e é uma função de x . Usando a condição inicial, v = 0 em y = 0 para a equação (1)

  0 = B h 2 ( 0 ) - ( 0 ) 3 3 + K ( x )     K ( x ) = 0  

Substitua 0 para K ( x ) na equação (1)

v = B h 2 y - y 3 3 … … ( 3 )

Portanto, a fórmula geral para a velocidade v é B h 2 y - y 3 3 .

Passo 4

b) Usando a condição de contorno na parede superior, v = v w em y = h na equação (2)

  v w = B h 2 × h - h 3 3     B = 3 v w 2 h 3  

Portanto, o valor de constante B é 3 v w 2 h 3 .

Resposta

a) v = B h 2 y - y 3 3

b) B = 3 v w 2 h 3

Exercícios de Livros Relacionados

As coordenadas polares esféricas ( r ,θ ,ϕ ) são definidas na Figura P 4.12 . As transformações cartesianas são x = r sen ⁡ θ cos ⁡ ϕ y = r sen ⁡ θ sen ⁡ ϕ z = r cos ⁡ θ A relação da continuidade cart
Um campo de velocidade bidimensional é dado por V = x 2 - y 2 + x i - ( 2 x y + y ) j em unidades arbitrárias. Em x ,y = ( 1 ,2 ) , calcule (a) as acelerações a x e a y , (b) o componente de velocidad
Um campo de velocidade idealizado é dado pela fórmula V = 4 t xî - 2 t 2 yj ^ + 4 x zk ^ î Esse campo de escoamento é permanente ou não permanente? Ele é bidimensional ou tridimensional? No ponto x ,y
Um modelo simples de escoamento para um bocal convergente bidimensional é a distribuição u = U 0 1 + x L v = - U 0 y L w = 0 (a) Faça um esboço de algumas linhas de corrente na região 0x / L1 e 0 y /
Quando uma válvula é aberta, o fluido escoa no duto divergente da Figura P4.8 de acordo com a aproximação V = i U 1 - x 2 L tanh ⁡ U t L Encontre (a) a aceleração do fluido em x ,t = ( L ,L / U ) e (b