Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 6.Problemas - Ex. 23
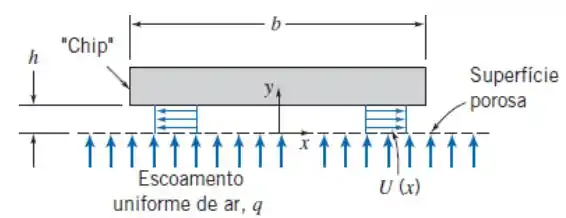
Um “chip” retangular de microcircuito flutua sobre uma fina camada de ar, com espessura h = 0,5 mm, acima de uma superfície porosa. A largura do chip é b = 40 mm, conforme mostrado. O seu comprimento, L, é muito grande na direção perpendicular ao plano da figura. Não há escoamento na direção z. Considere que o escoamento na direção x, na fresta sob o chip, é uniforme. O escoamento é incompressível e os efeitos de atrito podem ser desprezados. Use um volume de controle adequadamente escolhido para mostrar que U(x) = qx/h na fresta. Encontre uma expressão geral (2D) para a aceleração de uma partícula fluida na fresta em função de q, h, x e y. Obtenha uma expressão para o gradiente de pressão ∂p/∂x. Considere que a face superior do chip está sujeita à pressão atmosférica, e ache uma expressão para a força líquida de pressão no chip; essa força é voltada para cima ou para baixo? Explique. Determine a vazão q requerida (m3/s/m2) e a velocidade máxima, se a massa por unidade de comprimento do chip for 0,005 kg/m. Trace o gráfico da distribuição de pressão como parte da sua explicação sobre o sentido da força líquida.
Passo 1
Pessoal, vamos primeiro provar que . Tendo em vista que o escoamento é 2D, o fluido é incompressível e não há atrito.
Além disso, temos uma relação entre V e u, pois o volume deslocado na vertical é o mesmo que escoará pela horizontal. Veja o desenho:
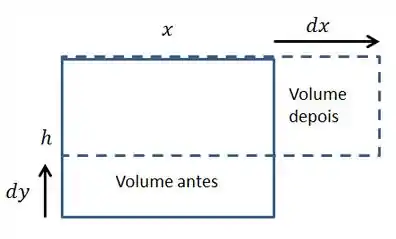
Considerando a multiplicação muito pequena, podemos desprezá-la. Então:
Derivando em função do tempo:
Passo 2
A equação da aceleração da partícula é dada pela equação:
A expressão em x é dada por:
Simplificando ():
De modo semelhante, temos para y:
Passo 3
Para escoamento 2D, a equação da continuidade é dada por:
Substituindo o valor de u, temos:
Para encontrar a velocidade , vamos usar o conceito:
Substituindo e integrando a expressão:
Como , ficamos com:
Agora vamos voltar para as equações das acelerações.
Em x, substituindo os valores, ficamos com:
Em y, substituindo os valores, ficamos com:
A equação geral da aceleração será dada então por:
Passo 4
Para encontrar o gradiente de pressão, vamos usar a equação de Euler em x:
Substituindo e sendo :
Fazendo a mesma coisa para y, o gradiente de pressão fica:
Substituindo e sendo :
Passo 5
A distribuição de pressão em x pode ser encontrada integrando a equação do gradiente:
Basta substituir e integrar a expressão. OBS: pelo desenho vemos que U(x) muda o sentido de escoamento no meio da placa. Portanto, vamos pegar metade do intervalo x=b/2 .
O gráfico da pressão será uma parábola com concavidade para baixo:
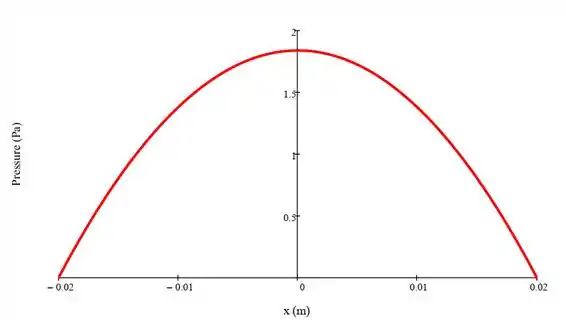
A equação geral da força é dada por:
Para a equação da força, podemos eliminar a pressão atmosférica da relação, pois todo o sistema está sob efeito da mesma. Substituindo os valores e lembrando que usamos apenas metade da placa, temos a expressão:
A força então está na vertical.
Passo 6
É dado que a massa do chip por unidade de comprimento vale 0,005kg/m. Para relacionar este parâmetro com a força vertical, vamos balancear com a força da gravidade:
Substituindo os valores:
Substituindo q na equação da velocidade:
Vemos que é uma reta, isto é, a velocidade máxima será dada quando x for o maior valor, neste caso x=b/2: