Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo Numérico - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 4.Problemas - Ex. 46

Deduza as equações de diferenças finitas nodais para as seguintes considerações.

(a) Nó (m,n) sobre um contorno diagonal sujeito à convecção com um fluido a uma temperatura T ∞ , com um coeficiente de transferência de calor h . Suponha ∆ x = ∆ y .

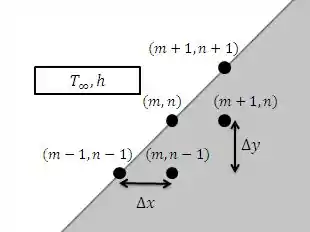
(b) Nó (m,n) na extremidade de uma ferramenta de corte cuja superfície superior está exposta a um fluxo térmico constante q 0 ' ' e a superfície diagonal está exposta a um processo de resfriamento por convecção com um fluido a T ∞ , com um coeficiente de transferência de calor h . Suponha ∆ x = ∆ y .

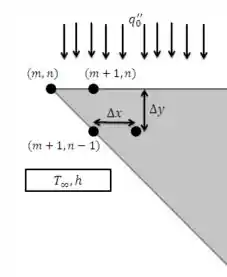
Passo 1

O item (a) nos pede para obter a equação de diferenças finitas para o ponto ( m , n ) . Para isso, vamos começar desenhando o volume de controle e as taxas de transferência de calor que agem sobre o sistema.

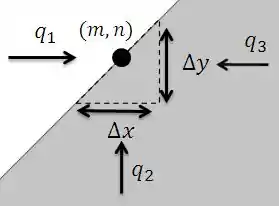
O balanço de energia considerando regime estacionário é:

E ˙ e n t - E ˙ s a í d a + E ˙ g e r = 0

E ˙ e n t = 0

q 1 + q 2 + q 3 = 0

Para o item (b) também devemos obter a equação de diferenças finitas para o ponto ( m , n ) em uma outra situação. De maneira análoga, começaremos desenhando o volume de controle e as taxas de transferência de calor:

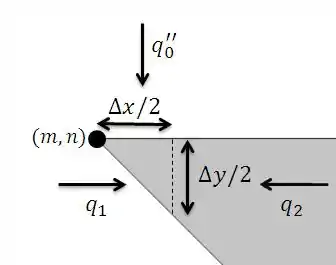
E o balanço de energia fica:

E ˙ e n t - E ˙ s a í d a + E ˙ g e r = 0

E ˙ e n t = 0

q 1 + q 2 + q 0 ' ' A = 0

Passo 2

Vamos agora descrever cada taxa separadamente para o item (a):

q 1 = q c o n v

q 1 = h A 1 ∆ T 1

q 1 = h ∆ x 2 + ∆ y 2 1 2 ∙ 1 T ∞ - T m , n

q 2 = q m , n - 1 → m , n

q 2 = k A 2 L 2 ∆ T 2

q 2 = k ∆ x ∙ 1 ∆ y T m , n - 1 - T m , n

q 3 = q m + 1 , n → m , n

q 3 = k A 3 L 3 ∆ T 3

q 3 = k ∆ y ∙ 1 ∆ x T m + 1 , n - T m , n

Substituindo no balanço de energia para o item (a):

h ∆ x 2 + ∆ y 2 1 2 ∙ 1 T ∞ - T m , n + k ∆ x ∙ 1 ∆ y T m , n - 1 - T m , n + k ∆ y ∙ 1 ∆ x T m + 1 , n - T m , n = 0

Como ∆ x = ∆ y :

h 2 ∆ x 2 1 2 ∙ 1 T ∞ - T m , n + k T m , n - 1 - T m , n + k T m + 1 , n - T m , n = 0

h 2 ∆ x T ∞ - T m , n + k T m , n - 1 - T m , n + k T m + 1 , n - T m , n = 0

h 2 ∆ x k T ∞ - T m , n + T m , n - 1 - T m , n + T m + 1 , n - T m , n = 0

h 2 ∆ x k T ∞ + T m , n - 1 + T m + 1 , n - 2 1 + h 2 ∆ x 2 k T m , n = 0

Passo 3

Vamos desenvolver agora as relações para as taxas de transferência de calor para o item (b):

q 1 = q c o n v

q 1 = h A 1 ∆ T 1

q 1 = h ∆ x 2 4 + ∆ y 2 4 1 2 ∙ 1 T ∞ - T m , n

q 2 = q m + 1 , n → m , n

q 2 = k A 2 L 2 ∆ T 2

q 2 = k ∆ y 2 ∙ 1 ∆ x T m + 1 , n - T m , n

q 3 = q 0 ' ' A 3

q 3 = q 0 ' ' ∆ x 2 ∙ 1

Substituindo no balanço de energia:

h ∆ x 2 4 + ∆ y 2 4 1 2 ∙ 1 T ∞ - T m , n + k ∆ y 2 ∙ 1 ∆ x T m + 1 , n - T m , n + q 0 ' ' ∆ x 2 ∙ 1 = 0

Supondo ∆ x = ∆ y :

h 2 ∆ x 2 4 1 2 T ∞ - T m , n + k 2 T m + 1 , n - T m , n + q 0 ' ' ∆ x 2 = 0

h 2 ∆ x 2 T ∞ - T m , n + k 2 T m + 1 , n - T m , n + q 0 ' ' ∆ x 2 = 0

h 2 ∆ x k T ∞ - T m , n + T m + 1 , n - T m , n + q 0 ' ' ∆ x k = 0

2 h ∆ x k T ∞ + T m + 1 , n - 1 + h 2 ∆ x k T m , n = - q 0 ' ' ∆ x k

Resposta

(a) h 2 ∆ x k T ∞ + T m , n - 1 + T m + 1 , n - 2 1 + h 2 ∆ x 2 k T m , n = 0 .

(b) 2 h ∆ x k T ∞ + T m + 1 , n - 1 + h 2 ∆ x k T m , n = - q 0 ' ' ∆ x k .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um longo cilindro sólido, com diâmetro D = 25 mm, é formado por um núcleo isolante que é coberto por um revestimento metálico altamente polido e muito fino (t = 50 μm), com condutividade térmica de k=
Determine a distribuição de temperaturas em t=30m i n para as condições do Problema 5.116 .(a) Use uma técnica de diferenças finitas explícita, com um incremento de tempo de 600s e um incremento no es
Seja o elemento combustível do Exemplo 5.11 . Inicialmente, o elemento está a uma temperatura uniforme de 250 ° C sem geração de energia. Subitamente, o elemento é inserido no núcleo do reator passand
Considere duas placas, A e B, que estão, cada uma, inicialmente isotérmicas e têm espessura L=5m m . As faces das placas são subitamente colocadas em contato em um processo de união. O material A é ac
Considere a folha metálica delgada que atua como malha de aceleração ( k=40W / ( m·K ) ,α=3×10 - 5m 2 / s , ε=0,45 ) , descrita no Problema 4.72. Desenvolva um modelo implícito de diferenças finitas p