Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo Numérico - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 4.Problemas - Ex. 42

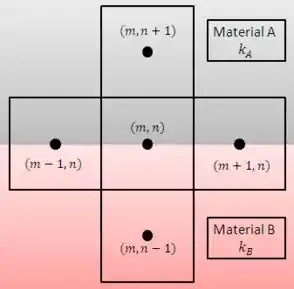
Determine as expressões para q ( m - 1 , n ) → ( m , n ) ,   q m + 1 , n → ( m , n ) ,   q m ,   n + 1 → ( m , n ) e q m ,   n - 1 → ( m , n ) , na condução associada a um volume de controle que abrange dois diferentes materiais. Os volumes de controle têm L unidades de comprimento para dentro da página. Escreva a equação de diferenças finitas para o ponto nodal (m,n) sob condições de regime estacionário.

Passo 1

O exercício nos pede para definir as taxas de transferência de calor de cada um dos pontos até o ponto central ( m , n ) . Para isso, vamos começar desenhando um volume de controle e as taxas de transferência de calor que atravessam o sistema:

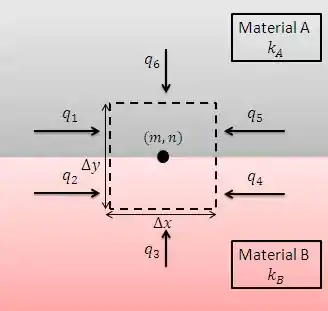
O balanço de energia para essa situação de regime estacionário é:

d E d t = E ˙ e n t - E ˙ s a í d a + E ˙ g e r

Como não temos nenhum fluxo de calor saindo do volume de controle e não há geração de energia a equação se reduz à:

0 = E ˙ e n t

0 = q 1 + q 2 + q 3 + q 4 + q 5 + q 6

Passo 2

Vamos agora determinar cada uma das taxas separadamente:

q 1 = k A A 1 L 1 ∆ T 1

q 1 = k A ∆ y 2 ∙ L ∆ x T m - 1 , n - T m , n

q 2 = k B A 2 L 2 ∆ T 2

q 2 = k B ∆ y 2 ∙ L ∆ x T m - 1 , n - T m , n

Como q 1 e q 2 vêm da mesma direção podemos escrever:

q 1 + q 2 = q m - 1 , n → ( m , n )

q m - 1 , n → ( m , n ) = k A ∆ y 2 ∙ L ∆ x T m - 1 , n - T m , n + k B ∆ y 2 ∙ L ∆ x T m - 1 , n - T m , n

q m - 1 , n → ( m , n ) = ( k A + k B ) ∆ y 2 ∙ L ∆ x T m - 1 , n - T m , n

Continuando:

q 3 = q m , n - 1 → ( m , n )

q 3 = k B A 3 L 3 ∆ T 3

q 3 = k B ∆ x ∙ L ∆ y T m , n - 1 - T m , n

q 4 = k B A 4 L 4 ∆ T 4

q 4 = k B ∆ y 2 ∙ L ∆ x T m + 1 , n - T m , n

q 5 = k A A 5 L 5 ∆ T 5

q 5 = k A ∆ y 2 ∙ L ∆ x T m + 1 , n - T m , n

Analogamente como fizemos com q 1 e q 2 :

q 4 + q 5 = q m + 1 , n → ( m , n )

q m + 1 , n → ( m , n ) = k B ∆ y 2 ∙ L ∆ x T m + 1 , n - T m , n + k A ∆ y 2 ∙ L ∆ x T m + 1 , n - T m , n

q m + 1 , n → ( m , n ) = ( k A + k B ) ∆ y 2 ∙ L ∆ x T m + 1 , n - T m , n

Por fim

q 6 = q m , n + 1 → ( m , n )

q 6 = k A A 6 L 6 ∆ T 6

q 6 = k A ∆ x ∙ L ∆ y T m , n + 1 - T m , n

Passo 3

Voltando para o balanço de energia:

k A + k B ∆ y 2 ∙ L ∆ x T m - 1 , n - T m , n + k B ∆ x ∙ L ∆ y T m , n - 1 - T m , n + k A + k B ∆ y 2 ∙ L ∆ x T m + 1 , n - T m , n + k A ∆ x ∙ L ∆ y T m , n + 1 - T m , n = 0

k A + k B ∆ y 2 ∆ x T m - 1 , n + T m + 1 , n - 2 T m , n + k B ∆ x ∆ y T m , n - 1 - T m , n + k A ∆ x ∆ y T m , n + 1 - T m , n = 0

Esta é a equação genérica de diferenças finitas para o ponto nodal ( m , n ) em regime estacionário.

Resposta

As equações de taxa de transferência serão:

q m - 1 , n → ( m , n ) = ( k A + k B ) ∆ y 2 ∙ L ∆ x T m - 1 , n - T m , n

q m , n - 1 → ( m , n ) = k B ∆ x ∙ L ∆ y T m , n - 1 - T m , n

q m + 1 , n → ( m , n ) = ( k A + k B ) ∆ y 2 ∙ L ∆ x T m + 1 , n - T m , n

q m , n + 1 → ( m , n ) = k A ∆ x ∙ L ∆ y T m , n + 1 - T m , n

E a equação de diferenças para o ponto ( m , n ) em regiem estacionário será:

k A + k B ∆ y 2 ∆ x T m - 1 , n + T m + 1 , n - 2 T m , n + k A ∆ x ∆ y T m , n + 1 - T m , n + k B ∆ x ∆ y T m , n - 1 - T m , n = 0

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Seja a condução bidimensional, em regime estacionário, em uma seção transversal quadrada com temperaturas superficiais especificadas. Determine as temperaturas nos nós 1, 2, 3 e 4. Estime a temperatur
Uma folha metálica delgada, com espessura 0,25 mm e um padrão de orifícios extremamente pequenos, serve como uma grade de aceleração para controlar o potencial elétrico de um feixe de íons. Tal grade
Considere usar a metodologia experimental do Problema 4.70 para determinar a distribuição de coeficientes de transferência de calor ao redor de um aerofólio de forma complexa.Levando em conta a conduç
Um sistema comum para o aquecimento de uma grande área superficial consiste em passar ar quente através de dutos retangulares localizados abaixo da superfície. Os dutos são quadrados e posicionados na
Seja o Problema 4.69. Um engenheiro deseja medir a temperatura superficial do fino revestimento, pintando ele de preto (ε = 0,98) e usando um dispositivo de medição infravermelho para, de forma não in