Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 2.Problemas - Ex. 38
Condução unidimensional, sem geração de energia e em regime estacionário, está ocorrendo em uma casca cilíndrica com raio interno e raio externo . Sob quais condições a distribuição de temperaturas linear mostrada é possível?
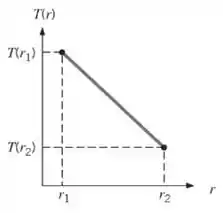
Passo 1
Nessa questão, nós temos uma casca cilíndrica em condições de estado estacionário sem geração de energia. Então temos a seguinte imagem:
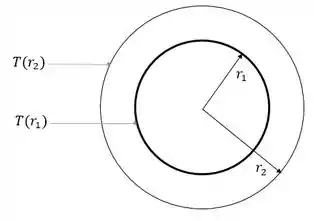
A partir disso, queremos descobrir sob quais condições é possível uma distribuição linear de temperatura.
Passo 2
Para resolver essa questão, vamos assumir que estamos em condição de estado estacionário, a condução é unidimensional e não há geração interna de energia. Nas condições indicadas, a equação do calor em coordenadas cilíndricas é:
Se a distribuição de temperatura é uma função linear de , então o gradiente de temperatura é constante e essa equação se torna:
O que implica ou . A única maneira de haver uma distribuição linear de temperatura na casca cilíndrica é se a condutividade térmica variar inversamente com