Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 6.Problemas - Ex. 27

Considere o campo de escoamento V → = A x 4 - 6 x 2 y 2 + y 4 i ^ + B x 3 y - x y 3 j ^ ;     A = 2   m - 3 s - 1 , B é uma constante e as coordenadas são medidas em metros. Determine B para este escoamento ser incompressível. Obtenha a equação para a linha de corrente que passa através do ponto (x, y) = (1, 2). Deduza uma expressão algébrica para a aceleração de uma partícula fluida. Estime o raio de curvatura da linha de corrente em (x, y) = (1, 2).

Passo 1

Pessoal, temos um escoamento em 2D e incompressível, além do campo de velocidade. Então, vamos usar a equação 5.3 do livro, que aborda a equação da continuidade para estas condições:

∂ u ∂ x + ∂ v ∂ y = 0

Onde:

u = A x 4 - 6 x 2 y 2 + y 4

v = B x 3 y - x y 3

Substituindo os valores, temos:

∂ A x 4 - 6 x 2 y 2 + y 4 ∂ x + ∂ B x 3 y - x y 3 ∂ y = 0

A 4 x 3 - 12 x y 2 + B x 3 - 3 x y 2 = 0

4 A + B x 3 - 3 x y 2 = 0

Então, para a expressão ser valida para quaisquer valores de x e y:

4 A + B = 0

B = - 4 A

B = - 8   m - 3 s - 1

Passo 2

A equação da aceleração da partícula em x é dada pela equação:

a x = D u D t = u ∂ u ∂ x + v ∂ u ∂ y + w ∂ u ∂ z + ∂ u ∂ t

Podemos simplificar a expressão e ficamos com:

a x = u ∂ u ∂ x + v ∂ u ∂ y

Substituindo os valores, temos:

a x = A x 4 - 6 x 2 y 2 + y 4 ∂ A x 4 - 6 x 2 y 2 + y 4 ∂ x + B x 3 y - x y 3 ∂ A x 4 - 6 x 2 y 2 + y 4 ∂ y

a x = A 2 x 4 - 6 x 2 y 2 + y 4 [ 4 x 3 - 12 x y 2 ] + A B x 3 y - x y 3 - 12 x 2 y + 4 y 3

Como B = - 4 A :

a x = A 2 x 4 - 6 x 2 y 2 + y 4 4 x 3 - 12 x y 2 - 4 A 2 x 3 y - x y 3 - 12 x 2 y + 4 y 3

Após o algebrismo acima podemos escrever da seguinte forma:

a x = 4 A 2 x x 2 + y 2 3

No ponto (1,2), a aceleração em x é dada por:

a x = 4 ( 2 ) 2 1 1 2 + 2 2 3

a x = 2000   m / s 2

Passo 3

A equação da aceleração da partícula em y é dada pela equação:

a y = D v D t = u ∂ v ∂ x + v ∂ v ∂ y + w ∂ v ∂ z + ∂ v ∂ t

Podemos simplificar a expressão e ficamos com:

a y = u ∂ v ∂ x + v ∂ v ∂ y

Substituindo os valores, temos:

a y = A x 4 - 6 x 2 y 2 + y 4 ∂ B x 3 y - x y 3 ∂ x + B x 3 y - x y 3 ∂ B x 3 y - x y 3 ∂ y

a y = A B x 4 - 6 x 2 y 2 + y 4 [ 3 x 2 y - y 3 ] + B 2 x 3 y - x y 3 [ x 3 - 3 x y 2

Como B = - 4 A :

a y = - 4 A 2 x 4 - 6 x 2 y 2 + y 4 [ 3 x 2 y - y 3 ] + 16 A 2 x 3 y - x y 3 [ x 3 - 3 x y 2

Após o algebrismo acima podemos escrever da seguinte forma:

a y = 4 A 2 y x 2 + y 2 3

No ponto (1,2), a aceleração em y é dada por:

a y = 4 2 2 2 1 2 + 2 2 3

a y = 4000   m / s 2

O vetor aceleração total vai ser dado por:

a → = 4 A 2 x x 2 + y 2 3   i ^ + 4 A 2 y x 2 + y 2 3 j ^

a → = 4 A 2 x 2 + y 2 3 [ x i ^ + y j ^ ]

a → = 2000 i ^ + 4000 j ^   m / s 2

Passo 4

A inclinação da linha de corrente é dada por:

d y d x = v u = - A x y A x 2 2 = - 2 y x

Temos então a expressão:

d y d x = B x 3 y - x y 3 A x 4 - 6 x 2 y 2 + y 4 = - 4 A x 3 y - x y 3 A x 4 - 6 x 2 y 2 + y 4

d y d x = - 4 x 3 y - x y 3 x 4 - 6 x 2 y 2 + y 4

Vamos fazer uma substituição de variável para resolver esta integral:

Seja

t = y x

d t d x = d y x d x = 1 x d y d x + y d 1 x d x = 1 x d y d x - y x 2

d t d x = 1 x d y d x - y x 2

d y d x = x d t d x + y x

d y d x = x d t d x + t

Igualando as equações, temos:

d y d x = x d t d x + t = - 4 x 3 y - x y 3 x 4 - 6 x 2 y 2 + y 4

Dividindo os termos do lado direito por x 4 :

x d t d x + t = - 4 y x - y x 3 1 - 6 y x 2 + y x 4

x d t d x + t = - 4 t - t 3 1 - 6 t 2 + t 4

x d t d x = - t + 4 t - t 3 1 - 6 t 2 + t 4

x d t d x = - t - 6 t 3 + t 5 + 4 t - 4 t 3 1 - 6 t 2 + t 4

x d t d x = - 5 t - 10 t 3 + t 5 1 - 6 t 2 + t 4

Separando as variáveis:

1 - 6 t 2 + t 4 5 t - 10 t 3 + t 5 d t   = - 1 x d x

Integrando esta equação, veja que a expressão grande em t obedece a regra da cadeia:

1 5 ln ⁡ 5 t - 10 t 3 + t 5 = - ln ⁡ x + C

ln ⁡ 5 t - 10 t 3 + t 5 + 5 ln ⁡ x = C

ln ⁡ 5 t - 10 t 3 + t 5 x 5 = C

Aplicando exponencial:

5 t - 10 t 3 + t 5 x 5 = c

Voltando com o valor t = y x :

y 5 - 10 x 2 y 3 + 5 x 4 y = c

No ponto (1,2), temos:

2 5 - 10 1 2 2 3 + 5 1 4 2 = - 38

y 5 - 10 x 2 y 3 + 5 x 4 y = - 38

Passo 5

O módulo da aceleração total no ponto (1,2) vai ser dado por:

a = a x 2 + a y 2

a = 4472,14   m / s 2

A componente normal neste ponto pode ser encontrada a partir do ângulo entre a aceleração e velocidade:

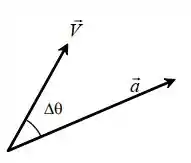
O ângulo da velocidade em relação a origem é dado por:

θ v e l = arctan ⁡ v u = arctan ⁡ - 4 A x 3 y - x y 3 A x 4 - 6 x 2 y 2 + y 4

Substituindo no ponto (1,2):

θ v e l = arctan ⁡ - 4 1 3 2 - 1 2 3 1 4 - 6 1 2 2 2 + 2 4

θ v e l = arctan ⁡ ( - 3,43 )

θ v e l = - 1,287   r a d

θ v e l = - 73,74 º

O ângulo da aceleração em relação a origem é dado por:

θ a c e l = arctan ⁡ a y a x = arctan ⁡ 4 A 2 y x 2 + y 2 3 4 A 2 x x 2 + y 2 3

θ a c e l = arctan ⁡ y x

Substituindo no ponto (1,2):

θ a c e l = arctan ⁡ 2

θ a c e l = 63,4 º

Então, o ângulo entre os dois vetores será:

∆ θ = θ a c e l - θ v e l

∆ θ = 63,4 - ( - 73,74 )

∆ θ = 137 , 14 º

Por definição, a componente normal da aceleração é perpendicular ao vetor velocidade. Então podemos encontrar pela expressão:

a n = a   s e n ( ∆ θ )

a n = 4472,14   s e n ( 137,14 )

a n = 3042   m / s 2

O raio de curvatura pode ser obtido através da equação da aceleração normal:

a n = V 2 R

O modulo da velocidade no ponto (1,2) será:

V 2 = u 2 + v 2

V 2 = A x 4 - 6 x 2 y 2 + y 4 2 + - 4 A x 3 y - x y 3 2

V 2 = 2 1 - ( 6 ) 1 2 2 2 + 2 4 2 + - 4 ( 2 ) 1 3 2 - 1 ( 2 ) 3 2

V 2 = - 14 2 + 48 2

V = 50 m s

Então, a curvatura será de:

R = 50 2 3042

R = 0,82   m

Resposta

B = - 8   m - 3 s - 1

a → = 4 A 2 x 2 + y 2 3 [ x i ^ + y j ^ ]

a x = 2000   m / s 2

a y = 4000   m / s 2

y 5 - 10 x 2 y 3 + 5 x 4 y = - 38

R = 0,82   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

5.71 Considere novamente o perfil de velocidade senoidal usado para modelar a componente x velocidade para a camada-limite no problema 5.12. Despreze a componente vertical da velocidade. Avalie a circ
5.85 Considere o escoamento induzido por pressão entre placas paralelas e estacionárias, separadas pela distância b. A coordenada y é medida a partir da placa inferior. O campo de velocidade é dado po
5.65 Ar escoa em uma folga estreita, de altura h, entre dois discos paralelos muito próximos, através de uma superfície porosa, conforme mostrado. Use um volume de controle, com superfície externa loc
5.88 Considere o escoamento induzido por pressão entre placas paralelas, separadas pela distância 2b. A coordenada y é medida a partir da linha de centro do canal entre as placas. O campo de velocidad
5.63 Ar escoa em uma folga estreita, de altura h, entre duas placas paralelas muito próximas, através de uma superfície porosa, conforme mostrado. Use um volume de controle, com superfície externa loc