Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 4.Problemas - Ex. 25
Considere o escoamento incompressível e permanente através do dispositivo mostrado. Determine o módulo e o sentido da vazão volumétrica através da porta 3.
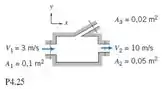
Passo 1
Nesse problema temos um fluxo através do dispositivo. O objetivo é encontrar a taxa de fluxo de volume na porta 3. Para isso, utilizaremos a equação:
Como todo problema da mecânica dos fluidos, fazemos as seguintes considerações:
fluxo constante, incompatível e uniforme.
Passo 2
Então para a caixa, vamos ter:
Observe que assumimos saída na porta 3, portanto:
Assim, o sinal negativo indica que o fluxo na porta 3 está para dentro e a vazão na porta 3 é de para dentro.
Resposta
Exercícios de Livros Relacionados
O campo de velocidades de um escoamento é dado por v x = 3 y e v y = 2 .O movimento é variado ou permanente?Determinar o campo das acelerações.Determinar os módulos da velocidade e aceleração no ponto
A placa da figura tem uma área de 2m 2 e espessura desprezível. Entre a placa e o solo existe um fluido que escoa formando um diagrama de velocidades bidimensional dado por v = 20 y v m á x ( 1 - 5 y
No sistema da figura, A 3 = 0,5m 2 , ρ 3 = 0,4k g / m 3 e os fluidos são gases. No sistema da figura, o óleo fornecido pela bomba mantém o pistão parado. O óleo escoa através da folga entre o pistão e
O tanque da figura abaixo permanece em nível constante. O escoamento na calha tem uma seção transversal quadrada e é bidimensional, obedecendo à equação v = 3 y 2 . Sabendo que o tanque B tem 1m 3 e é
O esquema a seguir corresponde à seção longitudinal de um canal de 25c m de largura. Admitindo escoamento bidimensional e sendo o diagrama de velocidades dado por v = 30 y - y 2 ( ye mc m ; ve mc m /