Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 4.Problemas - Ex. 15

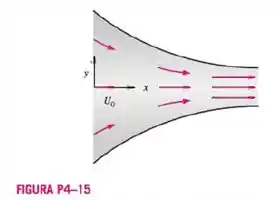
Considere o escoamento em regime permanente, incompressível e bidimensional através de um duto convergente (Figura P4-15). Um campo de velocidade aproximado simples para esse escoamento é

V → = u , v = U 0 + b ⋅ x ⋅ i → - b ⋅ y ⋅ j →

onde U 0 é a velocidade horizontal em x = 0 . Observe que essa equação ignora os efeitos viscosos ao longo das paredes, mas é uma aproximação razoável na maior parte do campo de escoamento. Calcule a aceleração material das partículas de fluido que passam através desse duto. Dê sua resposta de duas maneiras: (1) como componentes da aceleração a x e a y e (2) como vetor aceleração a → .

Passo 1

O enunciado quer que a gente calcule o campo de aceleração a → a partir de um campo de velocidade V → que o próprio enunciado informou. Como a aceleração material a → é igual à derivada material da velocidade D V → D t , podemos calcular a → derivando a equação de V → dada pela questão.

No entanto, a questão quer primeiro que a gente calcule as componentes a x e a y da aceleração. A equação 4 - 11 do livro calcula esses dois valores.

a x = ∂ u ∂ t + u ⋅ ∂ u ∂ x + v ⋅ ∂ u ∂ y + w ⋅ ∂ u ∂ z

a y = ∂ v ∂ t + u ⋅ ∂ v ∂ x + v ⋅ ∂ v ∂ y + w ⋅ ∂ v ∂ z

onde u é a componente do eixo x da velocidade V → , v é a componente do eixo y da velocidade V → e w é a componente do eixo z da velocidade V → . Como o escoamento é bidimensional a componente do eixo z w da velocidade vale zero. Logo:

a x = ∂ u ∂ t + u ⋅ ∂ u ∂ x + v ⋅ ∂ u ∂ y

a y = ∂ v ∂ t + u ⋅ ∂ v ∂ x + v ⋅ ∂ v ∂ y

Passo 2

O enunciado diz que a componente do eixo x da velocidade u vale:

u = U 0 + b ⋅ x

A componente do eixo y da velocidade v vale, segundo a questão:

v = - b ⋅ y

As derivadas parcias de u e v em relação ao tempo são nulas, porque elas não dependem do tempo t .

∂ u ∂ t = 0

∂ v ∂ t = 0

As derivadas parciais de u e v em relação a x e y valem:

∂ u ∂ x = ∂ U 0 + b ⋅ x ∂ x       ⟹       ∂ u ∂ x = b

∂ u ∂ y = ∂ U 0 + b ⋅ x ∂ y       ⟹       ∂ u ∂ y = 0

∂ v ∂ x = ∂ - b ⋅ y ∂ x       ⟹       ∂ v ∂ x = 0

∂ v ∂ y = ∂ - b ⋅ y ∂ y       ⟹       ∂ v ∂ y = - b

Passo 3

Substituindo essas equação das derivadas parciais nas fórmulas de a x e a y , encontramos:

a x = ∂ u ∂ t + u ⋅ ∂ u ∂ x + v ⋅ ∂ u ∂ y       ⟹       a x = 0 + U 0 + b ⋅ x ⋅ b - b ⋅ y ⋅ 0

a x = U 0 ⋅ b + b 2 ⋅ x

a y = ∂ v ∂ t + u ⋅ ∂ v ∂ x + v ⋅ ∂ v ∂ y       ⟹       a y = 0 + U 0 + b ⋅ x ⋅ 0 - b ⋅ y ⋅ - b

a y = b 2 ⋅ y

Passo 4

O enunciado também pede para a gente encontrar a aceleração a → na forma vetorial. A equação abaixo mostra como é a aceleração na forma vetorial.

a → = a x ⋅ i → + a y ⋅ j →

Substituindo a x e a y na equação acima, achamos:

a → = a x ⋅ i → + a y ⋅ j →       ⟹       a → = U 0 ⋅ b + b 2 ⋅ x ⋅ i → + b 2 ⋅ y ⋅ j →

Resposta

1       a x = U 0 ⋅ b + b 2 ⋅ x

a y = b 2 ⋅ y

2       a → = U 0 ⋅ b + b 2 ⋅ x ⋅ i → + b 2 ⋅ y ⋅ j →

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O campo da velocidade para uma linha de vórtices no plano r θ (Figura P 4 - 38 ) é dado por u r = 0u θ = K r Onde K é a intensidade da linha de vórtices. No caso com K = 1.0m / s 2 faça o gráfico de c
O campo da velocidade para a rotação de corpo rígido no plano r θ (Figura P 4 - 37 ) é dado por u r = 0u θ = ω r Onde ω é o módulo da velocidade angular ( ω → aponta para a direção z). No caso com ω =
O campo de velocidade para uma linha de fontes no plano r θ (Figura P 4 - 39 ) é dado por u r = m 2 π r u θ = 0 Onde m é a intensidade da linha de fontes. No caso com m 2 π = 1.0m 2 / s , faça um gráf
Considere o campo de velocidade em regime permanente, incompressível e bidimensional do Problema 4 - 35 ( a ) Calcule a aceleração material no ponto ( x = 2m ,y = 3m ) ( b ) Esboce os vetores aceleraç
Um campo de velocidade bidimensional, incompressível e em regime permanente é dado por V → = u , v = 1 + 2.5 x + y i → + - 0.5 - 1.5 x - 2.5 y j → Onde as coordenadas x e y estão em m e o módulo da ve