Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo Numérico - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 5.Problemas - Ex. 131

Considere a operação de colagem descrita no Problema 3.115 , que foi analisada sob condições de regime estacionário. Agora, entretanto, o laser será usado para aquecer a película durante um período de tempo determinado, criando uma situação de aquecimento transiente como

mostrado na figura.

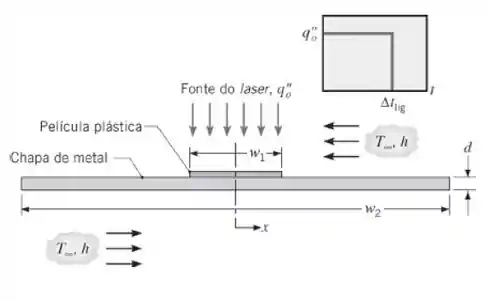
A chapa de metal se encontra inicialmente a 25 ° C e o laser fornece um fluxo uniforme de 85.000   W / m 2   durante um intervalo de tempo de Δ t l i g   =   10   s . As dimensões e as propriedades termofísicas do sistema permanecem as mesmas, porém o coeficiente convectivo para o ar ambiente a 25 ° C é agora de 100   W / ( m 2   ·   K ) e w 1   =   44   m m . Usando um método implícito de diferenças finitas com Δ x   =   4   m m e Δ t   =   1   s , obtenha os históricos das temperaturas, para 0   ≤   t   ≤   30   s , no centro e na aresta da película, T ( 0 ,   t ) e T ( w 1 / 2 ,   t ) , respectivamente, para determinar se o adesivo é satisfatoriamente curado acima de 90 ° C por 10   s e se a sua temperatura de degradação igual a 200 ° C é ultrapassada.

Passo 1

Vamos lá! Nosso problema pede o histórico de temperatura para o intervalo de tempo dado e um incremento de 10   m m , mas antes não vamos esquecer do nosso velho esboço pra facilitar nosso problema.

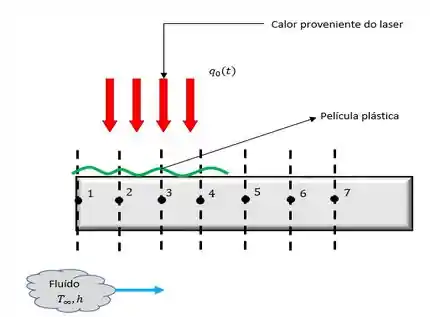
Agora precisamos fazer nossas famosas considerações. Hehe (u.u)

I - C o n d u ç ã o   u n i d i m e n s i o n a l

I I - P r o p r i e d a d e s   c o n s t a n t e s

I I I - C o e f i c i e n t e   c o n v e c t i v o   u n i f o r m e   n a s   s u p e r f i c i e s   s u p e r i o r   e   i n f e r i o r

I V - R e s i s t ê n c i a   t e r m i c a   e   m a s s a   d o   p l a t i c o   d e s p r e z í v e i s

V - T o d a   a   l u z   p r o v i n i e n t e   d o   l a s e r   é   a b s o r v i d a

Passo 2

Vamos lá! vamos considerar um nó como um volume de controle e vamos fazer o balanço de energia para ele pra chegarmos a nossa equação do método das diferenças finitas para um nó intermediário temos:

E ˙ e n t r a - E ˙ s a i = E ˙ a c u

q m - 1 + q m + 1 + q c o n v = M c p ⋅ T m p + 1 - T m p Δ t

k d ⋅ T m - 1 p + 1 - T m p + 1 Δ x + k d ⋅ T m + 1 p + 1 - T m p + 1 Δ x + q 0 ' ' Δ x + 2 h Δ x T ∞ - T m p + 1 = ρ Δ x d c p ⋅ T m p + 1 - T m p Δ t

T m p = 1 + 2 F 0 + 2 B i ⋅ F 0 T m p + 1 - 2 F 0 T m + 1 p + 1 - 2 F 0 ⋅ B i ⋅ T ∞ - F 0 ⋅ Q

Onde:

F 0 = α ⋅ Δ t Δ x 2 = 1,757 ⋅ 10 - 5 m 2 s ⋅ 1   s 0,004   m 2 = 1,098

B i = h Δ x 2 d k = 100 W m 2 ⋅ K ⋅ 0,0128   m 60 W m ⋅ K = 0,0213

Q = q 0 ' ' Δ x 2 d k = 85.000 W m 2 ⋅ 0,0128   m 60 W m ⋅ K = 18,133   K - 1

Passo 3

Agora ele pede o histórico de temperatura para o centro e arestas da película, ou seja, para o nó 1 e 5 , normalmente podemos resolver isso em forma de tabela, mas devido à natureza da questão fica melhor fazer com gráfico.

Assim usando o método de inversão de matrizes, que é apresentado no capítulo 4 , sendo mais especifico na seção 4.5 , assim usando os dados que encontramos e nossas equações, nosso gráfico vai ficar assim.

P.S: Pode desenvolver em qualquer software de sua preferência.

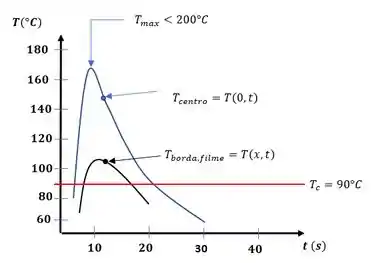
Analisando nosso gráfico temos que o centro está totalmente curado pois passou por um intervalo superior a 10 segundos em uma temperatura acima da temperatura de cura, já a aresta passou aproximadamente 8 segundos, 20 % a menos que o necessário.

Como no centro a temperatura não atingiu a temperatura de degradação, o ideal é aumentar o tempo de exposição ao laser um pouco, o suficiente para elevarmos atingirmos a cura na aresta da película, mas sem prejudicar o centro.

Isso é tudo pessoal! \o/

Resposta

Não é satisfatório, pois a aresta não realiza o processo de cura nas arestas, a temperatura de degradação não é atingida, o ideal é aumentar o tempo de exposição para sanar o problema.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

113 – Uma chaminé passando gases quentes de exaustão tem uma área de seção transversal quadrada de 300 mm de lado. As paredes são construídas de tijolos refratários de 150 mm de espessura com uma cond
114 – Elementos de aquecimento elétrico de pequeno diâmetro dissipando 50W/m são usados para aquecer um prato de cerâmica de condutividade térmica 2W/m.K. A superfície de cima do prato está exposta ao
94 – A função Der(T,t) de IHT pode ser usada para representar a derivada temperatura-tempo da equação 5.75. Neste problema nós usaremos a função Der para resolver o Exemplo 5.12.(A) Mostre, usando o m
103 – Considere a nacela da turbina eólica no Exemplo 1.3. A nacela é formada de um material compósito termoplástico de espessura L=20 mm. A condutividade térmica, a densidade, e o calor especifico do
95 – Considere o coletor solar do Problema 3.89. Depois de alcançar uma operação em condição de estado estacionário com q”rad=800 W/m2, o fluxo de radiação liquido para a superfície é rapidamente redu